ダイマー模型を組合せ論から考える~ダイマー模型の持つ性質~
2021.05.18

2021年4月28日、理学部数理科学科の中嶋 祐介助教による学生向け談話会「ダイマー模型とその周辺」を開催しました。
中嶋助教は、まず始めに「可換環論」と「特異点論」が研究分野であることを紹介。これらの分野の問題を、環の表現論や組合せ論といった他の数学分野の手法を使って調べているそうです。今回はあまり予備知識を必要としない組合せ論の話を中心に研究を紹介されました。
中嶋助教は、まず始めに「可換環論」と「特異点論」が研究分野であることを紹介。これらの分野の問題を、環の表現論や組合せ論といった他の数学分野の手法を使って調べているそうです。今回はあまり予備知識を必要としない組合せ論の話を中心に研究を紹介されました。
次にダイマー模型について考えるために必要な知識について説明がありました。ダイマー模型とは「トーラス上に書かれた二部グラフで、辺同士が頂点以外で交差しないもの」と定義されています。トーラスとはドーナツ型の図形で、右の図のように正方形に簡略化して表す事ができます。この正方形は“赤色同士、青色同士の辺がそれぞれつながっている”とみます。つまり、この正方形をくるっと丸めて青色の辺同士を接着させ、赤色も同様に接着させると、左図のドーナツ型の図形とみなせます。二部グラフとは、2種類の点と辺で表されるグラフで、同じ種類の点同士を線で結んでいないようなもののことをいいます。
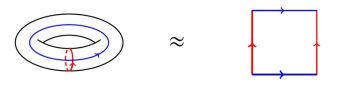
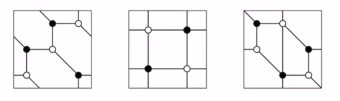
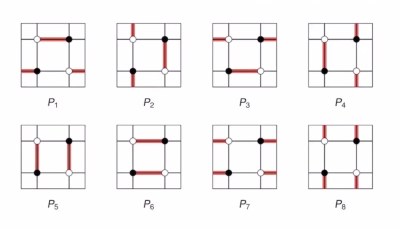
二部グラフは完全マッチングという辺の組合せを考えることが重要です。完全マッチングとは、共通の端点を持たない辺の部分集合で、任意の点はその部分集合の辺の端点となるようなものを指します。先ほどの例のダイマー模型を満たす完全マッチングは、合計で8個の組合せがあります。
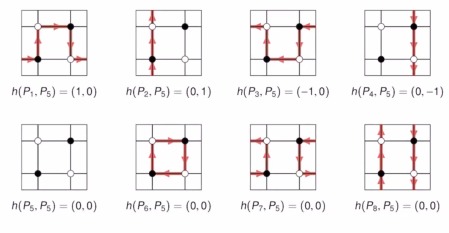
次に、完全マッチングの辺に白から黒方向への向きをつけて考えます。そして、二つの完全マッチングの差を考えます。引く側の完全マッチングはマイナスがついているので、矢印の向きを逆向きにして考えます。このようにして、トーラス上の向きがついているサイクルが得られます。図の正方形はトーラスなので、右の辺は左の辺と、上の辺は下の辺とつながっているので矢印は閉じていると考えられます。ひとつの完全マッチングを固定して、他の完全マッチングとの差を考えてみると、上の辺と右の辺の矢印の出入りの本数から図形を描くことができます。
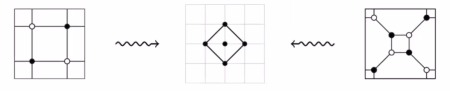
右の辺から出ていく矢印の本数から、入ってくる矢印の本数を引いたものをx座標、上の辺から出ていく矢印の本数から、入ってくる矢印の本数を引いたものをy座標として、片方を固定した完全マッチングの差をxy平面で表します。ダイマー模型の完全マッチングの差から得られる座標を全てxy平面にプロットし、それらを含む最小の凸集合を考えると多角形が現れます。これをダイマー模型の特性多角形といいます。
また、別のダイマー模型に対して同じようにして考えると、同じ特性多角形になることがあります。ここで、同じ特性多角形を持つダイマー模型にはどのような関係があるのかという疑問が浮かびます。同じ特性多角形を持つということは、何かしら数学的な共通点が存在するかもしれないからです。
そして、この疑問に対しては、ダイマー模型の変異ということを考えます。変異とは、対象の形は変えるが、本質的な数学的性質は変えない操作のことです。このような変異を通して、一つのダイマー模型が別のダイマー模型に結び付けられる時、これらのダイマー模型は同じ特性多角形を持つということが分かります。しかし、その逆である、同じ特性多角形を持つダイマー模型同士が、変異で移りあうのかは未解決だそうです。
また、別のダイマー模型に対して同じようにして考えると、同じ特性多角形になることがあります。ここで、同じ特性多角形を持つダイマー模型にはどのような関係があるのかという疑問が浮かびます。同じ特性多角形を持つということは、何かしら数学的な共通点が存在するかもしれないからです。
そして、この疑問に対しては、ダイマー模型の変異ということを考えます。変異とは、対象の形は変えるが、本質的な数学的性質は変えない操作のことです。このような変異を通して、一つのダイマー模型が別のダイマー模型に結び付けられる時、これらのダイマー模型は同じ特性多角形を持つということが分かります。しかし、その逆である、同じ特性多角形を持つダイマー模型同士が、変異で移りあうのかは未解決だそうです。
ダイマー模型の解説の後、中嶋助教が現在研究している内容について紹介がありました。特性多角形から、トーリック環と呼ばれる可換環や付随するトーリック多様体を定義でき、このトーリック多様体は一般に特異点を持ちます。この特異点は、ダイマー模型を使うことで特異点を解消することができます。
また、ダイマー模型の双対グラフとして、箙(えびら)と呼ばれる有向グラフを得ることができ、この箙から非可換クレパント特異点解消という対象が得られます。この非可換クレパント特異点解消は、導来圏と呼ばれる世界において、特異点の解消と結びついている対象で、中嶋助教は主にこのことについて研究を行っています。
また、ダイマー模型の双対グラフとして、箙(えびら)と呼ばれる有向グラフを得ることができ、この箙から非可換クレパント特異点解消という対象が得られます。この非可換クレパント特異点解消は、導来圏と呼ばれる世界において、特異点の解消と結びついている対象で、中嶋助教は主にこのことについて研究を行っています。
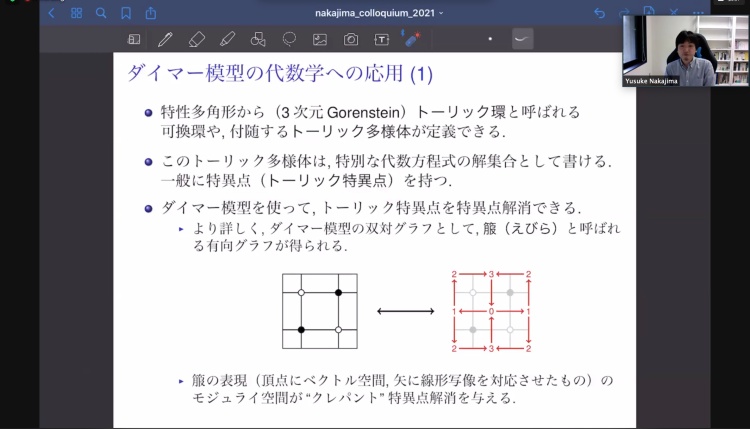

ダイマー模型の解説の後、中嶋助教が現在研究している内容について紹介がありました。特性多角形から、トーリック環と呼ばれる可換環や付随するトーリック多様体を定義でき、このトーリック多様体は一般に特異点を持ちます。この特異点は、ダイマー模型を使うことで特異点を解消することができます。
また、ダイマー模型の双対グラフとして、箙(えびら)と呼ばれる有向グラフを得ることができ、この箙から非可換クレパント特異点解消という対象が得られます。この非可換クレパント特異点解消は、導来圏と呼ばれる世界において、特異点の解消と結びついている対象で、中嶋助教は主にこのことについて研究を行っています。
また、ダイマー模型の双対グラフとして、箙(えびら)と呼ばれる有向グラフを得ることができ、この箙から非可換クレパント特異点解消という対象が得られます。この非可換クレパント特異点解消は、導来圏と呼ばれる世界において、特異点の解消と結びついている対象で、中嶋助教は主にこのことについて研究を行っています。
今回は中嶋助教による談話会「ダイマー模型とその周辺」をレポートしました。分かりやすくダイマー模型について解説されていたので、概要を理解することができました。今回の学びから更に考えを深めることができ、まだ分からないことや明確でないことが残っているということが、今後色々な性質を見いだせる可能性があることだと思い、そこに興味深さを感じました。
(学生ライター 理学部3年次 老田 将大)
