理学部 数理科学科 矢野　裕子 准教授

確率過程への誘い

　簡単なゲームから、物理学や経済学まで、時間とともに移り変わるものを表すための「確率過程」。確率と微積分が結び付いたことで生まれたこの数学は、20世紀に始まったばかりですが、さまざまな分野で応用されています。偶然現象の中には、私たちの直観とは異なるものがあります。このような現象を直観を排して数学的に説明するのが確率過程です。中でも奇妙な「逆正弦法則」が今回のキーワードです。さまざまな確率過程の研究を第一線で行う矢野裕子先生と一緒に、単純なゲームから確率過程の世界を眺めてみましょう。

コイン投げゲームをやってみよう

　はじめに、簡単なコイン投げのゲームを考え てみましょう。持ち点0からスタートし、コインを投げて表だったら勝ちで+ 1 点、裏だったら負けで−1 点とします。この簡単なコイン投げのゲームを繰り返して行います。

　結果を見やすくするために、簡単な式で書いてみます。

　　n回目のコイン投げの結果をX_nで表すことにします。このときX_nはの確率で+ 1か−1をとります。これに対し、Sn=X₁+X₂+…+X_nとすると、S_nがn回目の持ち点となります。持ち点が正の値であれば、勝ちの回数が負けの回数を上回っていることになります。要するに、勝ち越しの状態です。何度かコインを投げて、x座標がnでy座標がS_nの点をプロットして直線で結んだグラフを描くと、図1のようになります。この線がx 軸より上側にあるときを勝ち越しの期間、下側にあるときを負け越しの期間としましょう。このゲームを繰り返すとき、これらの期間は一体どのようになるでしょうか。

　勝ち越し期間，負け越し期間のいずれの期間も、全体のおよそ半分くらいになることがもっともらしいと思う人が多いのではないでしょうか。

　しかし、実際に何度かやってみると、予想外の結果が出てきます。コイン1 枚で実験できますので、皆さんで試しにやってみてください。

　結論を言いましょう。図2は、このコイン投げゲームを何度も繰り返したときの結果のひとつです。実は、勝ち越し期間と負け越し期間が同じくらいになることよりも、「ほとんど勝ち越し期間」か「ほとんど負け越し期間」のどちらかになることの方が起こりやすいのです。図2のようなグラフが現れることは決して珍しいことではないのです。

　このことを数学的に説明するのが、私の研究している「確率過程」です。

確率過程の誕生

　コイン投げのゲームから話を始めましたが、実際に確率論の起源のひとつは賭け事の問題であったと言われています。17 世紀に活躍し、さまざまな結果を残したパスカル（ BlaisePascal、1623 - 1662）とフェルマー（ Pierre deFermat、1607あるいは1608 - 1665）は、手紙のやりとりを通じて、途中で止めたゲームの賭け金の配分はどうしたらいいのか、などの問題に取り組みました。その後、確率論は、微分積分学やルベーグ積分論という数学と結び付いて飛躍的に発展しました。そして現れたのが、確率過程です。

　皆さんも中学、高校の数学で確率を習うと思いますが、確率過程という言葉はあまり馴染みがないかもしれません。確率過程とは、簡単にいえば「時間とともに変動する量を表現するもの」です。重要なのは、「時間」による移り変わりを見るという点です。

　確率過程は、20世紀にマルコフ（ AndreyAndreyevich Markov、1856-1922）らによって定式化されてきました。確率過程は物理学とも結び付いています。花粉を水に浮かべると観測される予測不可能な動きをブラウン運動と呼びますが、これも確率過程で表現することができます。

　さらに、日本の数学者・伊藤清（1915-2008）が伊藤の公式や伊藤解析といった手法を導き出すと、それに影響された多くの数学者が確率論を発展させて、経済の分野への応用も広がっていきました。今日では、伊藤解析は数理ファイナンスにおける重要なツールになっています。

　株価の動きから分子の運動まで、さまざまな分野で登場する確率過程。次では確率と微分積分がどのように関係するのかを見てみましょう。

微分積分と確率をつなげた先に

　高校では別々に習う微分積分と確率ですが、確率論を学ぶ上で微分積分学は極めて重要です。たとえば、最初に紹介したコイン投げで、試行を何回も繰り返すということを考えると、これは試行回数n →∞の極限を考えるということになります。このように確率論では極限を扱いますから、微分積分学は欠かすことができません。また、確率論では測度と呼ばれるものが使われますが、この測度とは、面積のように大きさを表した概念で、積分と深い関係があります。お馴染みの「期待値」も、実は積分そのものなのです。

　もう一歩踏み込んで考えてみましょう。先ほど確率といいましたが、これはどういう意味を持っているのでしょうか。

　確率論の最も重要なテーマのひとつに「大数の法則」と呼ばれるものがあります。簡単にいうと、ある試行を行ったときに事象Aが起こる比率は、試行を何度も繰り返すと事象Aが起こる確率に近づくという法則です。コイン投げの例でいえば、2、3回投げた程度ではすべて表だったり裏だったりと偏っているかもしれませんが、何度も繰り返すほど、表が出る比率はに近づいていきます。何回も投げれば2回に1回の割合で表が出るというのが確率の意味なのです。

　この法則を私たちは経験的に知っています。ここで注意したいことは、いま述べた法則は数学の定理としてはまだ不完全であるということです。先の法則の中で「近づく」という言葉を使いましたが、この「近づく」の意味があいまいです。これをはっきりさせないと数学の定理と呼ぶことはできません。確率論では、あいまいなこの法則はきちんと定式化して証明され、明瞭な数学の定理へと姿を変えます。確率論や確率過程論は、微分積分学などの解析学を駆使して偶然現象をうまく定式化した数学なのです。

逆正弦法則の不思議

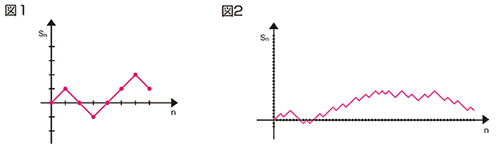
　コイン投げゲームでS_nの点を結んで出来たグラフ（図1、図2）は、確率論ではランダムウォークの道と呼ばれるものです。ランダムウォークは、日本語では酔歩や乱歩などと呼ばれます。名前の通り、酔っぱらいが千鳥足でふらふらと歩いたときの足取りのように見えます。

　ランダムウォークは、マルコフ過程と呼ばれる確率過程のひとつです。マルコフ過程は、現在の状態で条件付けたときに過去と未来とが独立であるという性質（マルコフ性）を持っています。たとえばコイン投げのモデルで、10回投げて10回表が出たら次は裏が出やすいかというとそうではなく、次の表裏もやはり確率は半々です。過去の情報を一切覚えていない、というのがマルコフ性の意味です。

　さて、逆正弦法則の詳しい説明に入りましょう。ランダムウォークの道がx軸よりも上側にある時間、下側にある時間をそれぞれ正側滞在時間、負側滞在時間といいます。先ほどのコイン投げゲームのときには勝ち越し期間，負け越し期間と呼んでいたものです。これらは、黒字の期間、赤字の期間と考えることもできますね。x軸を利益と損失が拮抗するラインだとすれば、正側滞在時間は「儲かっている時間」の合計だとみなせます。

　ランダムウォークの道を描いたとき、正側滞在時間と負側滞在時間は半々になりそうな気がしますが、最初に紹介したように、このような私たちの予想は裏切られてしまいます。実際には、正側滞在時間の割合は、ちょうど半分のになるよりも、0か1に近いことの方がもっともらしいのです。

　この現象は「逆正弦法則」に関係しています。1939年にフランスの数学者レヴィ（ PaulPierre Lévy、1886-1971）によって示されたこの結果は、厳密には極限定理として定式化されます。ランダムウォークの時間と空間を縮めると、ブラウン運動に収束します。確率過程の収束にはいろいろあって、ここでいう収束は正確には分布収束と呼ばれるものです。ランダムウォークの滞在時間も同様にブラウン運動の滞在時間に収束します。ブラウン運動の滞在時間の分布関数が逆正弦関数（正弦関数sin(x)の逆関数）を用いて表されることから、逆正弦法則という名が付いています。

　私の研究では、この逆正弦法則を一般化して、確率過程のどういう性質がこの法則の本質的な部分に関わっているのかを明らかにしようとしています。これまでに行った研究では、一次元拡散過程と呼ばれる確率過程に対して正側滞在時間を考え，その分布に関するいくつかの極限定理を発見し、証明しました。拡散過程というのは、ブラウン運動の道の連続性とマルコフ性に着目した拡張クラスです。

　確率過程には、道が連続ではないものもあります。たとえば、加法過程と呼ばれるものがそれです。加法過程のような道が連続でない確率過程の正側滞在時間を考えるためには、拡散過程のような道が連続な確率過程の場合とは異なる手法が必要です。そのような方法を探ることにも興味を持っています。

ブラウン運動

　花粉を水に浮かべて顕微鏡で見ると、その花粉から出た微粒子があちこちでたらめに動き回るという現象が見られます。このような不規則運動は、花粉のような生物由来のものに限らず、微細な粉末に普遍的に見られることを、植物学者・ブラウン（Robert Brown、1773-1858）が発見しました。この現象は、発見者の名前をとってブラウン運動と呼ばれています。それまでのニュートン力学では解析できないような、偶然的な運動です。この運動は1905年に相対性理論で有名なアインシュタイン（Albert Einstein、1879-1955）により数理モデルが提唱され、1923年に数学者ウィーナー（Norbert Wiener、1894-1964）によって、数学的に厳密に定式化されました。

アドバイス

　私たちは学校で数学の定理や公式を習います。まるで当たり前のことのように教わることもありますね。「こんなことも分からんのか」なんて先生に呆れながら言われたこと、ありませんか？（ 私はあります。）しかし本当は、定理や公式というものは、人間が何度も間違え、正すという数多の紆余曲折を経て、作られたものなのです。数学はとても人間らしい学問だと、私は思っています。微分積分学や確率論が発展していったときも、多くの数学者がいろいろな挫折や失敗を積み重ねています。その繰り返しの結果として、私たちには整理された綺麗な数学が見えているのです。不思議なもので、それまで難しく思えたことも、分かってしまった後では驚くほど簡単に見えてしまいます。でも思い出してください、分かるまでは難しかったのです。本当に理解するまでは、誰でも難しさを感じるものです。それから、難しさを感じる点は人によって違います。ですから、他人と比較することには何の意味もありません。数学を学ぶ上で重要なことは、分かるまでの自らの努力を怠らないということです。すぐに分からなくても構いません。悩んで苦しんでも、少しずつでも重ねる努力は、何ものにも代え難い自身の財産になります。