- HOME
- ����
- �T�C�G���X���e�N�m���W�[
- �t�[���G�������̐V���Ȑ��E —�P���ȎO�p���ŕ��G�Ȕg��\��—
�t�[���G�������̐V���Ȑ��E —�P���ȎO�p���ŕ��G�Ȕg��\��—
���w�� �����Ȋw�� ���� �_�I �y����
�P���ȎO�p���ŕ��G�Ȕg��\��
�@���ׂĂ̊��͎O�p���̖����̏d�ˍ��킹�ŕ\�����Ƃ��ł���\����������ƁA�݂Ȃ���͂ǂ��v���܂����H�u����Ȃ̉R���v�Ǝv���l������ł��傤���A�u����͂������v�u���̕��@��m�肽���v�Ƃ����l�����邱�ƂƎv���܂��B18���I�㔼����19���I�O���ɂ����āA���̖��Ɏ��g�̂��t�[���G�Ƃ����t�����X�̐��w�҂ł����B
�@�A�C�f�A���͈̂ȑO���炠��܂������A���̕��@���m���������̂��t�[���G�������̂ł��B���݂ł́u���ׂĂ̊��v�Ƃ����������ے肳��Ă��܂����A����͂ق�̈ꕔ�̗�O�I�Ȋ��ŁA���Z���݂̂Ȃ��K���悤�Ȋ��ł���u���ׂĂ̊��v��\�����Ƃ��ł���̂ł��B���̃t�[���G�̉�͊w���A�ނ����g�M���ۂ̖��ɂ��G��Ȃ���A�剺�_�I�搶�ɁA�킩��₷���������Ă��������܂����B
���オ���߂����w���_
�@�@18���I�㔼�A�C�M���X����Ƀ��[���b�p�ŎY�Ɗv�����N����܂����B���C�@�ւ̔����𒆐S�Ƃ���V���������Љ�̒��ŁA���w���抪�������傫���ϓ����܂��B�Y�Ɗv���ȑO�̐��w�́A�V�̂̉^���@���ȂǁA�ǂ��炩�Ƃ����ΐl�X�̓��퐶������͉������ꂽ�Ƃ���Ŏg����w��ł������A���̎�������ɂ��Ď������̐����ɖ��������ʂŕK�v�Ƃ����w�╪��ւƕϖe���Ă����̂ł��B
�@���C�@�ւ́A���C�𗘗p���ĔM�G�l���M�[���@�B�������߂̃G�l���M�[�ւƕϊ����铮�͋@�ւł��B�C�M���X�Ŋm���������̋Z�p�ɑ��āA�Ȋw�҂����͔M�Ƃ������ۂ𗝘_�I�ɐ������邱�ƂɊS���W�߂܂��B�t�����X�ł͔M���ۂ��𖾂��邽�߂̐��w���_�������ɋ��߂��܂����B1811�N�ɁA�p���Ȋw�A�J�f�~�[���u�M�`���̖@���̐��w�I���_�������A���̗��_�̎������ʂƂ̔�r�����ށv�Ƃ��������o���Ă��܂��B���̂悤�ɔM���ۂ��𖾂��鐔�w���_�͓����̉Ȋw�E���w�E�ɂƂ��čŏd�v�ۑ肾�����̂ł��B�Ƃ����̂��M���ۂ͓����̍Ő�[�̕������_�ł���j���[�g���͊w�ł͐����ł��Ȃ����̂���������ł��B
�@���̎���̗v���ɉ�����悤�ɓo�ꂵ���̂��A�t�����X�̐��w�҃W���Z�t�E�t�[���G�iJean Baptiste Joseph Fourier�A1768�|1830�j�ł����B�t�[���G�̓p���Ȋw�A�J�f�~�[�̖��ɉ��債�A���̘_���̓A�J�f�~�[��܂��l�����܂����B
�@1822�N�ɂ́w�M�̉�͓I���_�x���o�ŁB�M�`���̗��_�ƂƂ��ɔM���ۂ���͂�����@���m�������܂����B���ɉ��p���삪�L�����_�ŁA�����ł͔M���ۂ݂̂Ȃ炸�H�w�╨���w�̔��ɑ����ʂŎg���Ă���̂ł��B
�t�[���G�̖@��
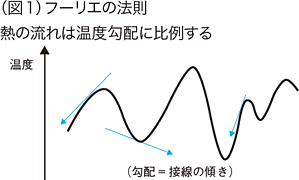
�@�@�M�`���Ɋւ��ăt�[���G�����������u�t�[���G�̖@���v�́A����܂ł̊ϑ������Ȃǂ��猩�o���ꂽ���̂ŁA�u�M�̓`�����͉��x���z�ɔ�Ⴗ��v�Ƃ������̂ł��B���x���z�Ƃ́A���x���z�i�M�̃O���t�j�̌X���̂��Ƃł��B���x�����}�ȂقnjX�����}�ɂȂ�A��葽���̔M���`���܂��B
�@�M�͉��x�̍����Ƃ��납��Ⴂ�Ƃ���ւƓ`����Ă������߁A�����艷�x�̍����Ƃ���ł́A�o�čs���M�̂ق��������̂ŁA���x���������Ă����܂��B�t�ɁA�����艷�x�̒Ⴂ�����ł́A�����Ă���M�̂ق��������Ȃ�A���x���オ���Ă����܂��B�������ʒu�A�c�������x�Ƃ��Đ}�ɂ���Ǝ��̂悤�ȃC���[�W�ɂȂ�܂��B
�@�t�[���G�͂���ɁA���̂悤�ȕ��G�Ȍ`���Ƃ�M�̃O���t�i���x���z�j�̎��ԓI�ȕω�����͂��邽�߂̕��@���m�����܂��B���ꂪ���G�ȃO���t���O�p���̏d�ˍ��킹�Ƃ��đ�������@�u�t�[���G�W�J�v�ł����B
���͖����̎O�p���̏d�ˍ��킹
�@�@�t�[���G�W�J���Љ��O�ɁA���̊�b�ƂȂ�O�p���K���Ă����܂��傤�B
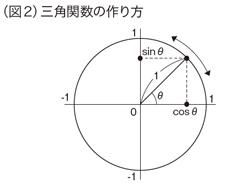
�@�O�p���́Ay=sin�ƁAy=cos�ƂȂǂƕ\����A���_�𒆐S�Ɏ��~���l���A���̉~������ړ�����_�ƌ��_�Ƃŗ^������O�p�`�̐����isin�j���邢�͗]���icos�j�̒l���Ƃ�܂��B
�@�����A�]���Ƃ�-1����1�̒l���Ƃ�܂��B1��360���Ō��̈ʒu�ɖ߂�A��������܂������l���J�Ԃ��u�������v�ł��B
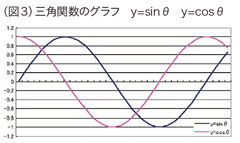
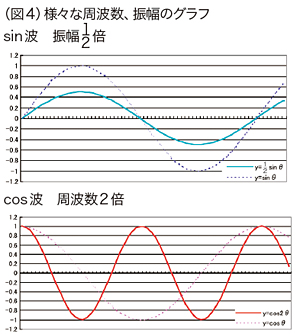
�@���ɁA���g���i�U�����j�ƐU����ω���������@�����Ă݂܂��傤�B���g���Ƃ͔g�̌J��Ԃ��̉̂��ƂŃO���t�ł͔g�̉����̋����ɑΉ����܂��i���g�����傫���ق�1�̔g�̉����͋��܂�܂��j�B�U���Ƃ͔g�̑傫���̂��ƂŃO���t�ł͔g�̏c���̑傫���ł��B�������̗��}�����܂��B
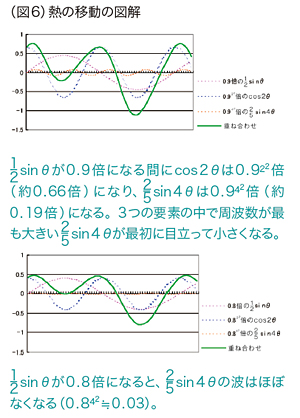
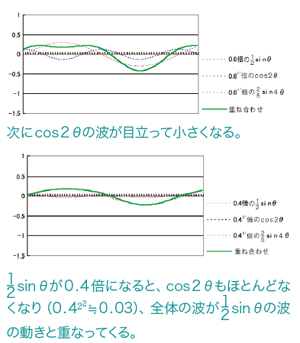
���̂悤�ɂ��āA��������g���A�U�������O�p������邱�Ƃ��ł��܂��B�����āA���̐}�̂悤�ɁA�������d�ˍ��킹��Ηl�X�ȕ��G�Ȕg��\�����Ƃ��ł���̂ł��B
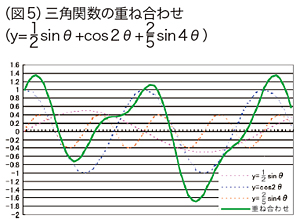
��̃O���t�͐��2�� ��
��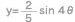 ���d�ˍ��킹�����̂ł��B�������A�\���O���t�ɂ���ẮA��葽���̔g���d�ˍ��킹�邱�ƂɂȂ�܂��B�t�[���G���m�����������@�ł͖����̑������킹�܂őz�肳��Ă��܂����A�ǂꂾ�����G�Ȕg�ł����Ă��A�����������킳��悤�Ƃ��A��{�ƂȂ�g��y= sin�Ƃ�y=cos�Ƃ���ό`�����P���Ȕg�Ȃ̂ł��B
���d�ˍ��킹�����̂ł��B�������A�\���O���t�ɂ���ẮA��葽���̔g���d�ˍ��킹�邱�ƂɂȂ�܂��B�t�[���G���m�����������@�ł͖����̑������킹�܂őz�肳��Ă��܂����A�ǂꂾ�����G�Ȕg�ł����Ă��A�����������킳��悤�Ƃ��A��{�ƂȂ�g��y= sin�Ƃ�y=cos�Ƃ���ό`�����P���Ȕg�Ȃ̂ł��B
�@���̂悤�ɂ��āA�t�[���G�͗l�X�Ȍ`�̔g��P���ȎO�p���ɕ����邱�Ƃ��ł���Ǝ����܂����B����ɂ��A�M���ۂ��O�p����p���ĕ\�����Ƃɐ��������̂ł��B
�M�̓�������͂���
�@�u�t�[���G�̖@���v�Ɓu�t�[���G�W�J�v�Ƃ�p���邱�ƂŁA�ő̂ł��t�́E�C�̂ł��A�����ȋ�������n���\�ʂ̔M�ɂ�����܂ł́A�l�X�ȔM�̓������v�Z�ɂ�苁�߂邱�Ƃ��ł��܂��B
�@�S�̂̔M�̏�Ԃ��A���Ԃ��o�ɂ�Ăǂ̂悤�ɕω����Ă����̂���m�肽���Ƃ��ɂ́A��قǂ̃t�[���G�W�J�����܂��B�܂��A�M�̕��z��Ԃ��Ȑ��ŕ\�������̂��t�[���G�W�J���܂��B�v�f�ɕ�����ꂽ��ЂƂ̎O�p���͐U�������ԂƂƂ��Ɍ`���ێ������܂������Ȃ��Ă����܂��B���̏������Ȃ鑬�x�́A���g�����傫���قǑ����Ȃ�܂��isin�Ƃ�r�{�ɂȂ�Ƃ��ɁAsin n�Ƃ�rn2�{�ɂȂ�j�B
�@��ЂƂ͒P���ȎO�p���Ȃ̂ŔM�̎��ԕω����ȒP�ɋ��߂��܂��B�����āA���鎞���ɂ�����M�̏�Ԃ�\������ɂ́A���Ԃɔ����ĐU�����������Ȃ����e�X�P���ȎO�p�����Ăяd�ˍ��킹������̂ł��B�}6�́A�}5��������ԂƂ����ꍇ�̔M�̓`������}�ɂ������̂ł��B
�@���̂悤�ȍl�����͔M���ۂ����ł͂Ȃ��A���R�E�Ɍ�����l�X�Ȋg�U���ۂ̐����ɂ��p���邱�Ƃ��ł��܂��B
����ł����p�����t�[���G�̃A�C�f�A
�@�t�[���G�̉�͊w�́A�������̔��ɐg�߂ȂƂ���ł����p����Ă��܂��B���Ƃ��A�������ꂽ�e���r���Ȃǂ��瑗���Ă���e���r��W�I�̓d�g�́A�f�[�^�̎��g����ϊ����đ���o����Ă��܂��B�����āA��M�������ł��̓d�g����f�[�^�����ĉ摜�≹�����Č����Ă���̂ł��B
�@�܂��A�R���s���[�^�Ȃǂʼn摜�≹���𑗎�M����ۂɗp������f�[�^���k�̋Z�p�ɂ��t�[���G�̃A�C�f�A����������Ă��܂��B���Ƃ��A�摜�f�[�^���k�̏ꍇ�A���k����O�̉摜�f�[�^�́A�摜�̓_��ЂƂɂ��Ă��ꂼ��F��3�����i�ԁA�A�j�̔Z�W�̃f�[�^���܂܂�Ă��܂��B���̂��߈�ʂɃf�[�^�ʂ��傫���Ȃ��Ă��܂��܂��B�����ŁA�e�F�̔Z�W���z���ʒu�̊��Ƃ��A���̊��ɑ��ăt�[���G�ϊ����s�����ƂȂǂŃf�[�^�ʂ����������Ă��܂��B
�@�e���r�̓d�g�ɂ������Ă���f���ɂ��t�[���G�̃A�C�f�A����������Ă���̂ł��B�������������e���r���y����A�C���^�[�l�b�g�ʼn摜�≹������M������ł���̂́A���̓t�[���G�̔��������������炱���Ȃ̂ł��B
�g�s�b�N�X
����ȉ^�������ǂ����V��
�@�t�[���G�����܂ꂽ�̂̓t�����X�v�����O�Ƃ��������̎���ł����B���̂��߁A�t�����X�v���ƃi�|���I������ɁA�ނ̐l���͑傫���h���Ԃ��܂��B1789�N�A�x�l�f�B�N�g�h�̊w�Z�̏C���m�������t�[���G�́A�p���Ȋw�A�J�f�~�[�ɕ������̉��̌��ɂ��Ă̘_���𑗂��Ă��܂��B�������A���̘_���͓��N�ɖu�������t�����X�v���ɂ���āA����ނ�̂܂܂ɂȂ��Ă��܂��܂��B�v���̉e���ŏC���m�����߁A�̋��ŋ��t�ɂȂ����t�[���G�ł������A1795�N�A�G�R�[���E�m���}�����J�Z����ƁA�������Ƃ��ē��w���܂��B�����āA�G�R�[���E�|���e�N�j�[�N�ւƈڂ�A���u�t�߂�悤�ɂȂ�܂��B1798�N�ɂ́A�i�|���I���̃G�W�v�g�����ɐ��s����Ȋw�҂ɑI��A�G�W�v�g�������̏I�g�����ɔC������܂��B�������A�C�M���X�Ƃ̋���ɂ��t�����X�̓G�W�v�g��������g���Ă��܂��܂��B�t�[���G�́A�G�R�[���E�|���e�N�j�[�N�ւ̕��A����]���܂����A�i�|���I���ɐ�����r�������܂�āA�t�����X�암�̃C�[�[�����̒m���ɔC������܂��B1808�N�A�i�|���I������͒j�݂݈̎ʂ܂ł��炢�܂��B�������A����Ȃ��ƂɃi�|���I���̎��r��A�p���̓��v�ǂ̊�������ɁA���w�̌����ɏW���ł���悤�ɂȂ�̂ł��B���w�ȊO�ɂ����ʂȍ˔\���������t�[���G���A�������鎞��͂Ȃ��Ȃ����R�ɂ��Ă���܂���ł����B�������A�ŏI�I�ɂ͐��w�҂Ƃ��đ���Ȍ��т��c���܂����B
�t�[���G�̉e���������X�̐��w�E�����w���_
�@�t�[���G���M���ۂ����Ƃ��đ����A���̊��͎O�p���ɕ����邱�Ƃŕ\�����Ƃ��ł���Ǝ咣�������Ƃ́A���̌�̐��w�E�����w�̔��W�ɑ傢�Ɋ�^���邱�ƂɂȂ�܂��B�t�[���G�́u���ׂĂ̊��͎O�p�����������킹�邱�Ƃŕ\�����Ƃ��ł���v�Ƃ����咣�́A�����̐��w�E�ɂƂ��ďd�v�Ȗ���N�ƂȂ�܂��B����܂ł̐��w�ł́u���ׂĂ̊��v�Ƃ͉����A�܂��u�����̑������킹�v�Ƃ͉����������ɋc�_����Ă��܂���ł����B�t�[���G�̂��̖���N�����������ɂ��āA��̏W���_�A�ϕ��_�A�m���_�Ƃ����������̕��삪���W���Ă������ƂɂȂ�܂��B�܂��A�����̎��g�������ɕ���������̒����Ƃ����l��������A������閳�������̋�ԂƂ����T�O�����܂�A�q���x���g��ԂƂ����ʎq�͊w�̐����I��b�ւƂȂ�������A�ʎq�͊w�̕s�m�萫���������w�I�ɂ̓t�[���G��͂̕s�����Ƃ��ĕ\���ꂽ�肷��ȂǁA�����w�̔��W�ɂ�����ȉe�����y�ڂ��܂����B

���w�� �����Ȋw�� ���� �_�I �y����
- �v���t�B�[��
-
�����Ȋw���m�B���͔���`�g�U�������̐����I�����B�u����`�v�Ƃ͕����ʂ�u���`�ł͂Ȃ��v�Ƃ����Ӗ��ŁA������2�{�ɂ��Ă����ʂ���Ⴕ��2�{�ɂȂ�Ȃ��悤�Ȍ��ۂ������B���R�E�ɑ��݂��鑽���̌��ۂ͔���`�B�u�g�U�v�Ƃ́A�M�̓`�����ȂǁA���ĕ��z���Ă�����̂��肪��菭�Ȃ�����ȏ�Ԃւƕω����Ă������ƁB����`�ł��g�U���錻�ۂƂ��ẮA�`���a�̍L�������2��ނ̏�Ԃ���蓾������ɂ������Ԃ̋��ڂ̈ڂ�ς��Ȃǂ���������B�����g�̌�������ɂ��Ắu���w�҂��猩��Ή��p�I�ȕ���ł��邪�A�����w�ҁE�����w�҂��猩��Η��_�I����v�Ɛ��w�ƉȊw�Ƃ̂��傤�Nj��E��ɂ��镪��Ƃ̂��ƁB