ランダムに移動するとどの辺にたどりつくか

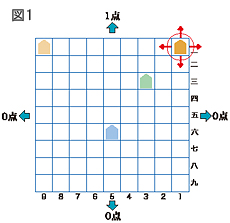
　次のようなゲームを考えます（図1）。まず、将棋の盤面のどこかのマスを選んで、そこにコマを置き、適当に前後左右に動かして行くとします。前後左右どの方向に動くのかは1/4の確率で決まり、指し手には決められません。盤面の端まで行って、外に出たらそこでゲーム終了です。
　あらかじめ、4辺ある盤面の端のどこに出るのかで点数を決めておきます。前に落ちたら1点、それ以外に落ちたら0点とするとき、どのマスからスタートしますか？
　おそらく、多くの人が盤面の前辺ぎりぎりのところを選ぶと思います。では、選ぶことができるマスを制限して、3三（右から3列目、前から3行目）のマス、5六のマス、9一のマスの3つからスタートするとしましょう。どのマスが一番得点できそうだと思いますか？ 9一は1/4で1点ですが、下手をすれば第一手で0点に落ちてしまいます。
　5六はほぼ真ん中だから0点になりにくそうですね。
　確率が分かっていて、点数も決まっているときには期待値を使って計算をします。1一のマスの期待値は(1一の期待値) = 1/4×1点+1/4×0点+1/4× (1二の期待値) +1/4× ( 2一の期待値)と表せます。
　この式をすべてのマスについて作ると81の式ができます。すべての式を連立させるとそれぞれの期待値を求めることができます。
　先ほどの場合ですと、3三の期待値は約0.40、5六が約0.18、9一は約0.49となります。この結果を見ると、9一からスタートするのが一番得点できそうだということになります。5六はもっとも低い結果しか期待できませんでした。

鉄板の温度を求める

　将棋盤のゲームで期待値を求める計算方法は「ランダムウォーク」と呼ばれるもので、先ほどのようなゲームの得点を計算する以外にも、様々なものを計算するときに便利な方法なのです。
　得点を温度に置き換え、将棋盤を鉄の板に置き換えると、4辺の温度が分かっているときの鉄板上のそれぞれの箇所の温度を計算することができます。前辺を100℃に保った湯に浸し、他の3辺を0℃に保った氷水に浸した鉄板の場合では、3三の箇所は約40℃、5六が約18℃、9一は約49℃と、将棋盤ゲームの期待値とまったく同じ結果が得られるのです。
　さらに、平面の鉄板だけではなく、立体の鉄球にも応用することができます。鉄球の表面の温度が分かっていれば、鉄球の中心の温度も計算から求められるのです。温度計を差し込むことができない鉄球の内部もこの方法で温度が分かるのです。
　純粋に数学の問題として、立体内部の温度が計算できると発見したのは、19世紀、ドイツのディリクレという数学者でした。このことから、立体内部の温度や平面の温度を求める問題を、彼の名前をとって「ディリクレ問題」と呼んでいます。
　ディリクレ問題を厳密に解くには微分方程式を用います。その解は「調和関数」と呼ばれる関数になります。
　「ディリクレ問題」はランダム似解を求めることができることを発見したのは角谷静夫という日本の数学者でした。ランダムウォークで用いるマス目をどんどん小さくしていけば、微分方程式で求められる解に限りなく近づいていくのです。ただ、マス目を小さくすると計算する連立方程式が何千、何万という式の連立になってしまうので、一般的にはコンピュータの力を借りて計算をしてもらいます。
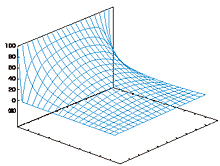
　図2を見てください。求められた鉄板の温度を目で見て分かるように図にしたものです。この図では、各地点の温度を高さとして表しています。このように図にすることで温度や熱の流れなどを視覚的に読み取ることができます。この図はコンピュータを使って描いたものですが、具体的なカタチで見てみたいならば、境界の温度を高さとして（たとえば100℃の辺なら高さ100ミリというように）作った枠組にシャボン玉の膜を張ったり、みかんを入れるためのネットを張ると、図と同じカタチを作ることができます。まさしく、調和関数を目で見ることができるのです。

純粋数学と宇宙物理学との出会い

　ディリクレ問題の解である調和関数について、少し話しておきましょう。
　ディリクレ問題の解法を含む、調和関数の理論は私の専攻する複素解析学という分野に属します。調和関数の理論は非常に応用範囲が広い理論です。先ほどの鉄板や鉄球のように物体内部での熱の問題を数式で表すことができるのはもちろん、「熱」を「エネルギー」や「重力」に置き換えることで、電磁場における磁力の強さや、大きな質量によって複雑に歪んだ宇宙空間での重力など、様々な場面に応用されています。まさに現代物理学にはなくてはならない数学の成果なのです。
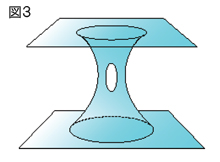
　最新の宇宙論のひとつである「超ひも理論」※1においても複素解析学は大活躍をしています。超ひも理論では、粒子の相互作用をひもの動きとしてとらえます。ひもが動いた軌跡は面となり、たとえば図3のような複雑な立体図形となります。このリーマン面とよばれる面の解析を行なうのに複素解析学の理論が使われます。以前にはリーマン面の理論は物理学と縁もゆかりもない理論と思われていました。しかし、現代では、最新の宇宙論において大いに応用されているのです。
　もともとは純粋な数学的な興味から出発した調和関数の理論ですが、物理学の発達に伴って、具体的な対象のある研究になりました。これは、数学者の整然とした論理を求める探究心が結果として実際の物理学に応用されたひとつの例となっています。

アドバイス

数学にも実験がある？

　高校生のみなさんに知っておいてもらいたいのは、高校と大学では数学の学び方が大きく変わるという点です。
　高校では、すでに検証された定理・証明を習います。もちろんすべて大切な内容で、大学で数学を学ぶ上での基礎となります。そして大学では、特に4年から大学院に進むと、自分たちで課題を見つけ、新しい定理を発見するという学びが中心になります。1年生から3年生では、そのための基礎知識を身につけ研究の仕方を学ぶのです。
　数学というと、実験とは無縁のように思われるかもしれませんが、今みなさんが高校で習っている数学の定理の多くは“先人”たちが繰り返し実験を行った成果です。数値計算や物理的な実験を重ね、仮説・予想を立て、そしてそれを検証して、証明を行い、新しい定理を生み出してきたのです。一つひとつの学習内容に過去の数学者の研究成果がつまっているのです。
　現在では、数値計算や実際の物理実験のかわりに、コンピュータを使って数値計算やシミュレーションなどの実験を行ないます。いろいろ条件を変えながら繰り返し計算を行うという実験の中から、新しい定理を探すのです。これは「実験数理」と呼ばれている数学の手法で、本学科の基本方針にもなっています。
　大学では、みなさんが“先人”の一人となり、新しい定理の発見に挑戦することになるでしょう。
　そんな大学での数学を楽しみにしておいてください。

理学部･数理科学科 石田 久教授

プロフィール

　専攻は複素解析学。特に、等角写像論、リーマン面の理論。京都大学在学中、複素解析学という分野に「目に見える」面白さがあると感じたのが、現在の分野に進むきっかけになった。現在でも講義では「目に見える数学」を心がけている。左の写真の「しゃぼん玉で作った曲面」もその一例。私立高槻高等学校OB。