研究テーマ
高校生に向けた研究内容の紹介
「なぜこんな形をしているのか」「なぜこんな現象が起こるのか」。世の中の色々な現象は、微分方程式を使って説明できます。微分方程式を解くことで、状態が「どのように変化するか」が分かります。また、関数の微分が0となる点を求めて形状を調べることを、高校で学びます。変分問題とはこれを拡張したもので、「関数の関数」の形状を調べる問題です。微分方程式を変分問題に書き換えることで、より複雑な現象を解析できます。
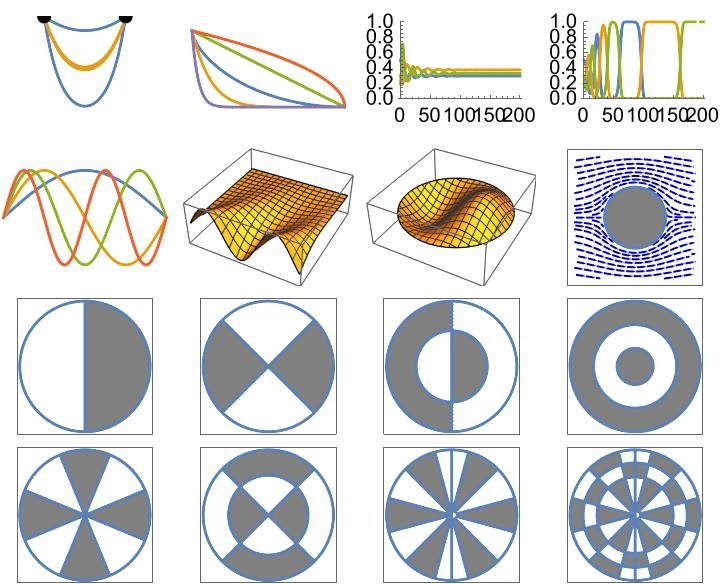
微分方程式と変分法
「なぜこんな形をしているのか」「なぜこのような現象が起こるのか」。世の中のさまざまな現象に関する疑問は、実は数学を使って説明することができます。私の研究室では、微分方程式を用いて、身近な現象を数学的に解析していきます。
方程式といえば、一般的に未知の“数”を解として求めるものですが、微分方程式では“関数”を求めます。状態は変化を伴い関数で表されるので、微分方程式を解くことで、現象が「どのように変化するか」が見えてきます。
例えば、やかんを火にかけるとどのくらいの速さで熱が伝わるかといった熱伝導や、物体が落下するときの空気中の抵抗力、感染者数や実効再生産数からウイルスの広がり方を算出するなど、おそらく皆さんが想像されるよりずっと身近なところで微分方程式を活用できます。
さらに「変分法」を用いて、微分方程式の解の存在や安定性を示す試みにも挑戦していきます。変分法とは、汎関数（関数の関数）を最大・最小化する手法であり、微分方程式を解くために有効なツールの一つです。変分問題に書き換えることで、これまで解けなかった微分方程式の解を導き出すことができ、より複雑な現象を解析することが可能になります。
大学で学ぶ数学は、「限られた時間で正しい答を求める」ことを目的とする高校までの数学とは違う面白さがあります。真剣に取り組めば、数学に関心を寄せるみなさんが、これまで積み上げてきた学びの一つのゴールとなるはずです。方程式を解いた先には何があるのか？？
一緒にその答えを探しましょう。
ゼミナール／研究室のテーマ
微分方程式と変分法
様々な自然現象は微分方程式を用いて数学的に定式化されます。このような微分方程式に対して、微分積分学で学ぶ極値を求める考え方を発展させた「変分法」を用いて、解の存在や安定性を示す研究を行います。
※特別研究とは、4年間の学びをもとに各自が研究テーマを設定し、教員の指導を受けて研究を深め、卒業研究としてまとめるもので、理学部での4年間の集大成となる重要な授業です。
ゼミ／卒業研究の紹介
私のゼミでは、微分方程式や変分問題、微分方程式を解くのに有用なフーリエ解析を学びます。卒業研究では、身に着けた手法を用いて、 様々な自然現象を解析します。学生の具体的な研究テーマは、吊り下げたネックレスの形・障害物があるときの水の流れ・楽器の音色と弦や膜の振動の関係・多種生物の競争や共存などです。微分積分学がどのように現象の解析に使われるか学び、それを人に伝えられることを目標としています。