研究テーマ
高校生に向けた研究内容の紹介
雪の結晶、草木や花々、動物や昆虫の体表模様、鳥や魚の集団運動、あるいは私たち人間の体など、身の回りには人の手を加えずとも自然と出来上がる模様や形が数多く存在し、我々の目を楽しませてくれます。このような特徴的なパターンや生き物らしさはどのように生まれるのでしょうか。
反応拡散方程式はそのような自然界でみられるパターン形成を記述するモデル方程式として広く用いられており、実際にシミュレーションをすると、コンピュータの中で様々なパターンが自発的に作られ、時事刻々変化する様子などが観察できます。
なかでも粒子状のパターンに注目し、その動きと背後にある数理構造との関係を調べることで、多彩な振る舞いのメカニズムや制御方法の解明に取り組んでいます。研究が進めば、人工細胞や人工生命を構築する際のヒントになるかもしれません。
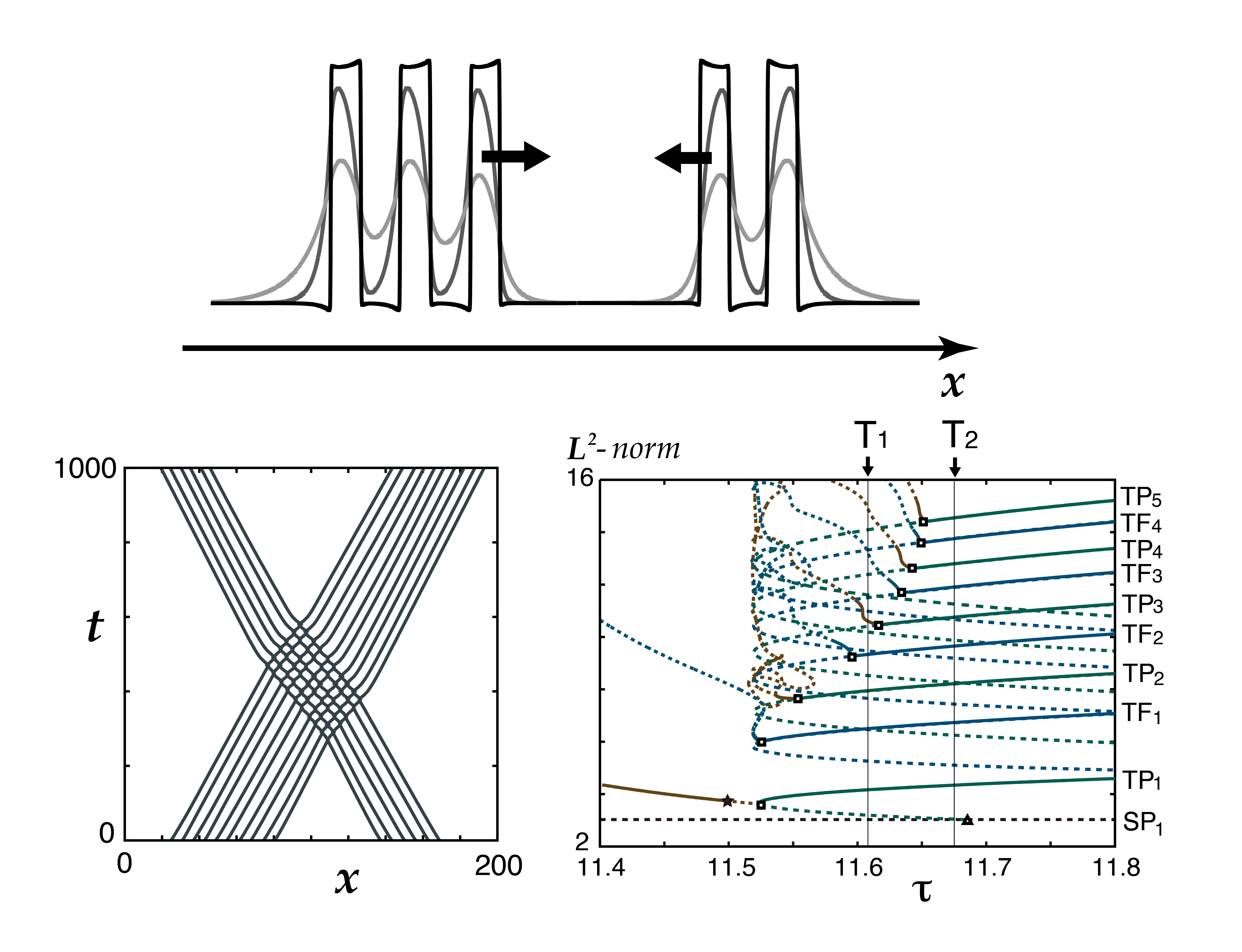
「雪の結晶」や「動物の模様」を数式で描いたら
雪の結晶や木の枝分かれ、動物や魚の体表パターンなど、模様や形が自然と生まれることを不思議に思ったことはありませんか？こういった時間変化する現象の多くは微分方程式で書かれ、その解として模様や形が表現されます。つまり、方程式や解の性質を調べることで、模様や形の背後にある“数学的な仕組み”を明らかにできるのです。
現象に応じて様々な方程式がありますが、特に自然界で見られるパターン形成のモデルとして幅広く利用されているのが「反応拡散方程式」。
計算機の父として知られるアラン・チューリングによって提唱され、以来、斑点や縞模様、枝分かれのようなパターンから、進行波やスパイラル、時空間カオスといったダイナミックに変化するものまで、実に多くのパターンが現れることが分かっています。
その中で特に注目しているのが、パルスやスポットのように空間的に局在化したパターン。数値シミュレーションでは自発的に動き回る様子がみられますが、複数個が集まったり環境からの影響を取り入れたりすることで、生き物のように多彩な振る舞いを見せます。
そのメカニズムを調べるため、力学系理論の観点からその数理構造を調べています。数学的な理解が深まれば、目で見ている複雑な現象の本質や一見異なる現象の共通点も見えてきて、また新たな現象を予見することも可能になります。
ゼミナール／研究室のテーマ
パターン形成の数理解析
結晶成長や川の流れのように、自然界には時々刻々変化するパターンが多くみられます。このような時間変化を記述する微分方程式について、力学系理論とシミュレーションによる解析を行い、パターン形成のメカニズムを探っていきます。
※特別研究とは、4年間の学びをもとに各自が研究テーマを設定し、教員の指導を受けて研究を深め、卒業研究としてまとめるもので、理学部での4年間の集大成となる重要な授業です。
ゼミ／卒業研究の紹介
「非線形ダイナミクスとカオス」（ストロガッツ著）や「カオス」（アリグッド・サウアー・ヨーク著）といった本を読みながら、力学系の基礎と現象への応用を学びます。時間とともに変化する現象がどのような数式で表され、それをどのように数学的に扱うかをコンピュータも使いながら勉強します。異なる現象であっても似た数式で記述できれば、同じような振る舞いをすることがわかると思います。数式で書ければ予測が可能なのか、シミュレーションは現象を正しく再現しているのか、といったことも考えていきます。
プロフィール
休みの日などは少し遠出することが多いですが、関西は古い街並みと新しいエリアが共存しており、名所や歴史的な建物、美術館など見どころも多いため、どこへ行っても楽しむことができます。五山の送り火で有名な大文字山（如意ヶ嶽）もちょっとしたハイキングコースになっており、京都の街並みが一望できておすすめです。
最近はギターも始めました。なかなか思うように上達しませんが、レパートリーも少しずつ増えて、練習の成果を実感しています。