本学理学研究科数学専攻を修了した藤田 淳希さん(現在:京都府立北稜高等学校)と理学部数理科学科の渡辺 達也 教授による、円筒管内に閉じ込められた石鹸膜の形状を記述する変分問題に関する学術論文が、シュプリンガー・ネイチャーの論文誌 Journal of Engineering Mathematicsに掲載されました。
掲載論文
著者:Atsuki Fujita, Tatsuya Watanabe
題目:Stability analysis of helical soap films for the Plateau problem confined to a cylindrical tube
雑誌:Journal of Engineering Mathematics 153(2025), Article number 3.
URL :https://doi.org/10.1007/s10665-025-10462-7
研究概要
与えられた閉曲線で囲まれた面積が最小の曲面を求める問題はプラトー問題と呼ばれ、古くから研究されてきました。例えば、針金で輪を作って石鹸水に浸すと、与えられた境界を持つ石鹸膜が形成されます。物理学的には、この石鹸膜は表面張力の作用によって面積が最小となる形状をとります。数学的には、この石鹸膜は平均曲率が0になるという性質を持ちます。このような曲面は極小曲面と呼ばれ、建築や化学素材にも応用されています。
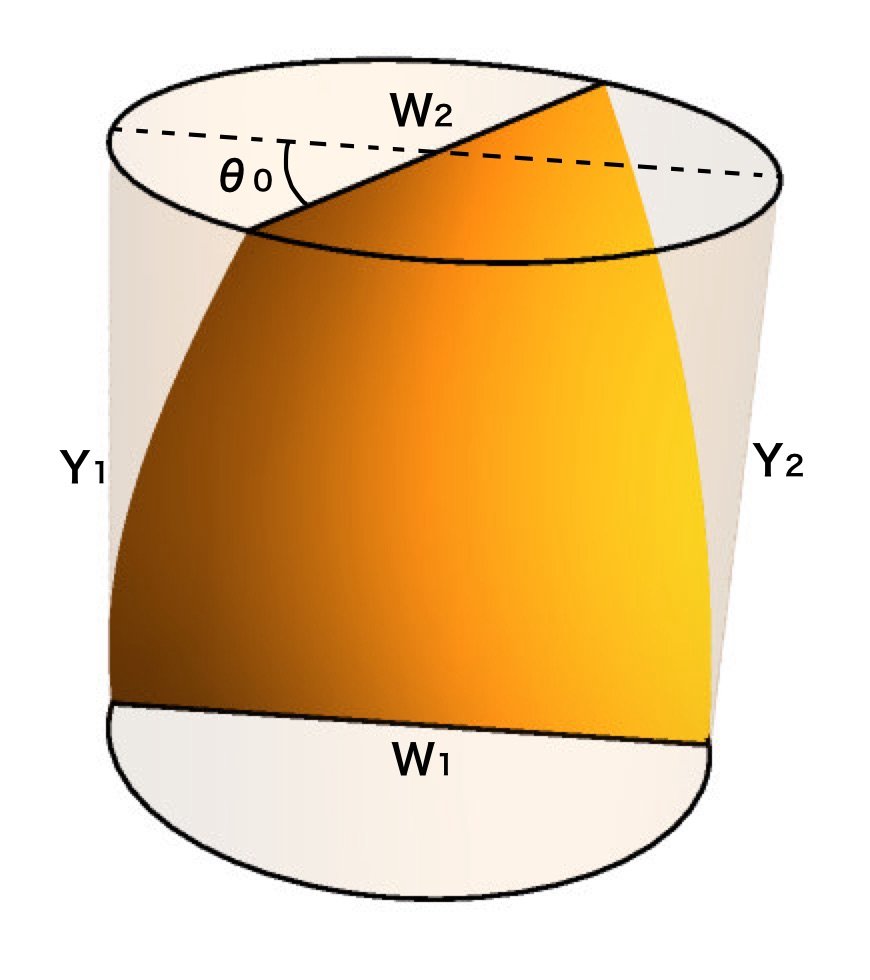
円柱管に閉じ込められた螺旋面
本論文では、CoxとJones(2014)によって提案された、円筒管内に閉じ込められた石鹸膜の形状を記述する変分問題を考察しました。特に付随するエネルギー汎関数の臨界点である、螺旋面の安定性と不安定性に着目します。SeguinとFried(2015)は、第二変分の安定性条件に関連する固有値問題を導出して、螺旋面の安定性についての結果を得ました。本研究では最小固有値をより詳細に解析することにより、円筒管の高さがある閾値を超えると、ねじれた螺旋面はすべて不安定になるという結果を証明しました。また、螺旋面が安定となるような円筒管の高さとねじりの角度のパラメータ領域に関して、既存の結果を改良することに成功しました。




