理学部 数理科学科 細野　雄三教授

世界観を覆した数学理論

　20世紀に生まれたカオス論は、科学の世界に大きなショックを与えました。「決定論的でも、予測不可能なものがある」カオスの持つこの特徴は、私たちの身近にも大きな影響を与えています。100％当たる天気予報はない。蝶の羽ばたきが竜巻を起こす。従来では考えられなかった世界像を提示した、カオスの世界。細野雄三先生に、この新しい学問を分かりやすく解説していただきました。

カオスが切り拓く世界観

　カオス論は、近代以降の決定論的世界観を揺るがす理論でした。

　ニュートンの運動方程式以来、最初の状態と状態の時間発展を記述する法則さえ得られれば、未来永劫あらゆる状態が予測できる、という考え方が自然科学を支配していました。この世界観の下では、複雑な事象の未来が予測できないのは、その事象を記述する式が複雑すぎて今の物理学では解き明かせないだけであり、将来その式さえ解明されれば必ず予測可能になる、と考えられていました。ところが、そのような見通しを否定したのがカオス論です。

　カオスの最も大きな特徴は、初期値に対する鋭敏性、すなわち「最初の状態がほんの少し違うだけで、将来非常に大きな違いを生む」というものです。わずかな誤差がやがて想像もつかないような大きな差になってしまい、混沌とした状態が生まれる。ここから「カオス」という名前がつきました。有効数字の最後の桁で切り捨ててしまうような小さな差が最終的に全く異なる結果を生んでしまうため、未来の状態を式から予測するのは事実上不可能です。カオス論は決定論的な世界観に則りながら、それでも予測できない未来があるという新しい見方を示しているのです。

　「カオス」という言葉は「混沌」と訳され、複雑なものを複雑に扱っているという印象を与えますが、非常に簡単な方程式からもカオス現象は現れます。複雑なものを見たときに、本当に複雑な要因のせいなのか、それとも単純な法則から生じたものなのか、改めて問い直さなければならない。そのような提言をしたという点で、カオス論は大きな意味を持つのです。

カオスの歴史

　　カオスは今でこそ様々な分野で扱われていますが、その起源は数学にあります。

　元々は、19世紀のポアンカレ（Jules-HenriPoincaré, 1854-1912）の「三体問題」に遡ります。これは、天体など相互作用する三つの物体の運動を扱う問題です。この解法を求める中で、ポアンカレは複雑な軌道が見られることに気づきました。当時、カオスという言葉はありませんでしたが、カオス現象の可能性はこの時期には発見されていたのです。

　そして、ポアンカレのこの研究は、バーコフ(George David Birkhoff , 1884-1944)やスメール(Stephen Smale, 1930-)達に引き継がれ、力学系の理論として発展し、その後のカオスの数学的研究の基礎を作ります。しかしながら、それは数学の世界の中だけで閉じていました。

　科学としての「カオス論」発展の契機を与えたのが、ロバート・メイ（Robert McCredieMay, 1936-）やエドワード・ローレンツ（Edward Norton Lorenz, 1917-2008）といった人々でした。

　x_n＋1=F（x_n）（n=0,1,2…）という式を考えてみましょう。高校数学でも学ぶように、初期値 x₀と式Fが決まれば、 x_nの値がx₁,x₂,x₃,…とずっと先まで次々と決まっていきます。すなわち、式Fがx_nからx_n＋1を決める「法則」を与えています。この、ある数に対して別のある数を対応させる法則Fを写像と呼びます。

　1970年代初頭、数理生態学者のロバート・メイは、生物の個体数の変動を調べるため、このFにF（x）=ax（1-x）（0≦x≦1）という法則を与えた式を計算機で解いていました。する、あるaの値で式が非常にでたらめな挙動をするという現象に出くわしたのです。これが、まさにカオスでした。このときのFはロジスティック写像と呼ばれています。見て頂ければわかるように、とても単純な法則です。

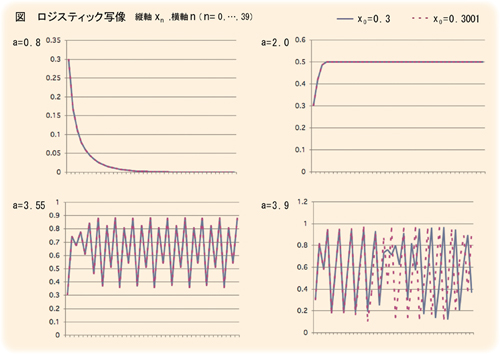
　実際にロジスティック写像の振る舞いを見て みましょう。（左図）0≦a≦1のとき、x_nは0に収束します。0≦a≦3のときも、一定の値（1-）に収束します。

　この方程式が収束する一点は不動点と呼ばれるもので、 x_n+1=x_nを解けば、簡単に上の収束値を求めることができます。

　ところが、aが3を少し超えると、一点には収束せず2周期を行ったりきたりします。さらにaを大きくしていくと４周期、8周期……と、2ⁿ周期で振動していきます。

　重要なのはここからです。aが3.570…というある値を超えると、この数列は全く不規則の、予測不可能なカオス領域に入ります。このとき、初期値x₀がほんの僅かに変わるだけで、数列は全く別なものになってしまうのです。左図を見てください。
a = 0.8, 2.0, 3.55のときとは異なって、a = 3.9 のときには初期値がわずか0.0001 異なっただけでn = 14 以降では全く違った振る舞いをしていることが分かります。

　これと同じことが、天気予報にも言えます。天気予報の式も難解な微分方程式で成り立っていますが、気象学者のローレンツはこれをよりシンプルな本質的な形に直して、1960年代前半に計算機を用いて数値計算を行いました。するとこの式も、初期値の僅かな違いで将来が全く予想できなくなってしまうという特徴を持っていたのです。ローレンツはこのことを「ブラジルで一匹の蝶が羽ばたくと、テキサスで竜巻が起きる」と表現しました（「バタフライ効果」）。

　二人のカオス現象の発見には、計算機が不可欠な役割を果たしました。そして、彼らには得られた計算結果からカオス現象を読み取る能力があったのです。その後のカオスの研究を含めて数学の分野でも、今や身近で容易に手に入る計算機は新たな発見と解析の道具として活躍していることを付け加えておきます。

身近に見られるカオス

　実際にカオスがどのような場所に見られるのか、いくつかの例を見てみましょう。

　感染症の伝播などを扱う反応拡散系というシステムがありますが、このシステムにおいて感染症が伝わっていく速さの波の先端（フロント波）の動きが、特別な感染メカニズムを仮定するとカオス的な振る舞いをします。反応拡散系は感染症だけでなく、生態学や化学反応の分野でもほとんど同じ式を用いますので、それらの分野にもカオスは見られます。

　もっと身近な例を挙げましょう。水道の蛇口を絞ると、水滴がぽつぽつと垂れる状態になります。このとき、水滴が落下するリズムは非常に不規則です。これもカオスです。

　もう一つ別の例で、パイこね変換というものを紹介します。これも写像の一つですが、そのイメージは経験的に理解しやすいと思います。パイ生地の一部においたバターを全体に均一に伸ばしたいときは、パイを二倍に引き伸ばしてから折りたたむという操作を繰り返すと、最初一カ所にあったバターが生地全体に行き渡っていきます。これもカオスの原理によるものです。

　このように身近なところに見られるカオスですが、実はその数学的定義は人によって異なり、誰もが納得するような定義はまだ存在しません。ここまで述べてきたのは、あくまでカオスの特徴です。

　新しい学問でありながら、世界観を一変させたカオス。今後、その更なる発展が期待されます。

決定論的世界と確率論的世界の橋架け

　カオスはランダムとは異なりますが、そこにはある種の繋がりがあります。

　コインを投げて表がでたらA、裏がでたらBとして、試行していくと、ランダムなAとBの文字列ができます。これは確率論的な世界の話で、一見カオスとは関係ないように見えます。ところが、このような確率論で定めた配列をカオスで再現することができるのです。ロジスティック写像のようにカオス的な振る舞いをする方程式には、 x_nが 0 ≦ x_n≦ 1-2を満たすときはA、 1-2＜x_n≦1を満たすときはBと書くという規則を定めたとき、あるランダムな文字列を再現するような初期値が必ず存在する。つまり、正しい初期値さえ分かれば、1回目から未来永劫、表か裏かがコイン投げにより決定された配列と同じ配列が方程式により得られることになります。ただし、その具体的な値は誰にもわかりません。

アドバイス

　高校時代は何でも好きなことをやって欲しいと思います。問題はその好きなことが見つけられるかどうかです。私自身は、数学も好きだったのですが、小説を読むのも好きで大学受験の際には文学部に行こうか理学部に行こうか迷っていたくらいです。高校時代には、どんなジャンルでも構いませんが、好奇心を持ってたくさん本を読んでほしいと思います。本を読むことにより自分の世界が広がり、自分のやりたいことや好きなことが何かを発見する手がかりが得られます。また、先生や友達といろいろ話しすることも手助けになるでしょう。好奇心のアンテナを張って、いろんなことに挑戦してください。