- HOME
- ����
- �T�C�G���X���e�N�m���W�[
- �|�A���J���\�z����ʑ��w�̐��E�ɐG���—4������Ԃɕ�����3��������—
�|�A���J���\�z����ʑ��w�̐��E�ɐG���—4������Ԃɕ�����3��������—
���w���@�����Ȋw�ȁ@�R�c�@�C�i ����
4������Ԃɕ�����3��������
�@2002�N11���A���E���̐��w�ҁA���Ɋw�̌����҂���������_�����E�F�u�T�C�g�ɓ��e����܂����B���̘_���̓��e�́A2000�N�ɃA�����J�̃N���C���w�����������w�j��ő�̓��Ƃ���100���h���̏܋���������7��̂�����1�u�|�A���J���\�z�v���ؖ��������̂������̂ł��B
�@1904�N�A�|�A���J���\�z�����ɏo����Ă���A�����̈ꗬ�̐��w�҂����̓��ɒ���ł͔s��Ă��܂����B���̂Ȃ��ɂ͂��������{�̐��w�҂��܂܂�Ă��܂��B����́A�F���̂��蓾��`�ɂ��Ă̗\�z�Ƒ����邱�Ƃ��ł��܂��B
�@���������A�ǂ�ȗ\�z�������̂ł��傤�B�R�c�C�i�搶�ɕ�����₷��������Ă��������܂����B
���I�̓��|�A���J���\�z
�@�n�܂�́A�t�����X�̐��w�҃A�����E�|�A���J���iJules-Henri Poincaré,1854-1912�j���_���̂Ȃ��Łu�������̋^�₪�ЂƂc��v�ƑO�u�����ď����o�������̈ꕶ�ł����B
�@���l�̂̊�{�Q���P�ʌ��݂̂ł���Ȃ���A���̑��l�̂�3�������ʂƓ����łȂ��\���͂���̂��낤���H
�@���̈ꕶ����ɁA�N���C���w�������ɂ���āu�~���j�A�����ܖ��v�Ƃ���100���h���̏܋���������ꂽ���w�j��ő�̓���1�u�|�A���J���\�z�v�ł��B
�@�u���l�́v��u��{�Q�v�A�u3�������ʁv�ȂǍ��Z���݂̂Ȃ���ɂ͕����Ȃ�Ȃ��p�ꂪ�o�Ă��܂��B�ЂƂ��������Ă����܂��傤�B
�u���l�́v�Ƃ́H
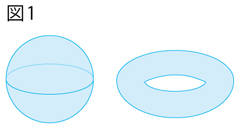
�@�@n�������l�̂Ƃ́A�}�`�̂ǂ̓_�ɂ����Ă��A���̂����߂��������l����ƁA���ʂ� n�������[�N���b�h��ԂƓ����悤�Ɍ�����}�`�̂��Ƃł��B�g�߂Ȑ}�`�ŗ��������ƁA�}1�̂悤�ȋ��ʁi���̕\�ʂ̋ȖʁA���̓����͊܂܂�Ȃ��j�╂���ւ̕\�ʁi���w�ł̓g�[���X�ƌĂԁj����\�I��2�������l�̂ł��B
�@���Ƃ��A�������͒n���Ƃ�������ȋ��ʂɏZ��ł��邱�Ƃ�m���Ă��܂����A�̂̐l�͕���ȑ�n�̏�ɏZ��ł���Ǝv���Ă��܂����B�����̋߂��������l����Ƃ��A����͂܂��� x���Ay���ŕ\����� 2 �������[�N���b�h��ԂƓ����悤�Ɍ����邩��ł��B�ł�����A���ʂ�2�������l�̂Ȃ̂ł��B�����Ӗ��ŁA�����ւ̕\�ʂ� 2�������l�̂ł��B���̑��ɂ��A2�������l�̂́A�����Ɏ�ނ�����܂��B���̂��ߑ��l�Ȍ`�����Ă���A�Ƃ����Ӗ��ŁA���l�̂Ƃ����̂ł��B
�@�����Łu���ʂ�g�[���X��3�����̐}�`�ł͂Ȃ��̂��H�v�Ƃ����^�₪�o�Ă��邱�ƂƎv���܂��B�m���ɂ��̐}�� 3������Ԃ̒��ɕ`����Ă��܂����A����͊O���̋�Ԃ� 3�������Ƃ��������ŁA�}�`���̂��̂� 2 �����Ȃ̂ł��B
�@�̂̐l����n�͕��ʂ��ƌ�����Ă����̂Ɠ������Ƃ��A���������Z��ł���F���ɂ��Ă������܂��B�������ɂ́A�ǂ��ɍs���Ă��Ax���Ay���Az���������ɂ̂тĂ���A���ʂ�3�������[�N���b�h��ԂɏZ��ł���悤�Ɍ����܂����A�ł��A�F���Ƃ���3�������l�̂̑S�̂̌`�͂ǂ��Ȃ��Ă��邩�͂킩��܂���B
�u��{�Q���P�ʌ��݂̂ł���v�Ƃ́H
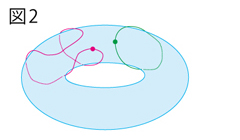
�@�u��{�Q�v�Ƃ����̂͑��l�̂̐����̂ЂƂŁA���l�̏�ɕ`���郋�[�v�̏W���̂��Ƃł��B�ʑ��w����Ƃ��鐔�w�҂̋����́A�ǂ̐}�`�Ƃǂ̐}�`�����ԂƌĂׂ�̂��A�Ƃ����Ƃ���ɂ���܂��B���̂��߂Ɋ�{�Q�Ƃ����������g���đ��l�̂ނ���肪����Ƃ��Ă���̂ł��B
�@2�������ʂ�2�����g�[���X�Ƃ̈Ⴂ���l����ƁA2�������ʂł͂����Ȃ郋�[�v���A���I�ȕό`�ɂ����1�_�ɏk�߂邱�Ƃ��ł��܂��B�܂�A1��ނ̃��[�v���������Ȃ��Ƃ������Ƃł��B������u��{�Q���P�ʌ��݂̂ł���i�����ȌQ�ł���j�v�ƌ����܂��B
�@���������ċ��ʂ𗷂���l���l���܂��B�n�_�Ŏ����Œ肵�A���R�Ƀ��[�v��`���܂��B���͈ړ������ɉ����Ă�����ł������Ȃ�܂����A���l�̂̊O�ɏo�邱�Ƃ͂ł��܂���B�����Ďn�_�܂Ŗ߂��Ă����瓯���_�ɌŒ肵�܂��B���̌�A������J���ƃ��[�v�͏��X�ɏk�܂�A�Ō�ɂ͕K��1�_�ɏW�܂�܂��B
�@2�����g�[���X�̏ꍇ�͎���قȂ�܂��B�g�[���X��̃��[�v�͋��ʏ�̃��[�v�Ɠ����悤��1�_�ɏk�߂邱�Ƃ��ł�����̂�����i�}2�s���N�̐��j�A�����̌��Ɉ��������茈����1�_�ɂ͏k�܂�Ȃ����[�v������܂��i�}2�̐��j�B
�@���̂悤�ɁA2�������ʂ�2�����g�[���X�Ƃł͊�{�Q�ɈႢ������A�Ⴄ��ނ̑��l�̂Ƃ��ĕ��ނł���̂ł��B
�u3�������ʁv���Ăǂ�Ȑ}�`�H
�@�@�|�A���J���\�z�̍Ō�́u�����v�Ƃ́A�}�`�������Ȃ����肵�Ȃ��ŁA�L������k�߂���̘A���I�ȕό`�ňڂ肠����悤�ȁA������ނ̐}�`�ł���Ƃ����Ӗ��ł��B����Ń|�A���J���\�z��ǂ݉������Ƃ��ł��܂����B������₷�����������Ă݂��
���ׂẴ��[�v��1�_�ɏk�߂���悤��3�������l�̂́A3�������ʁi�Ƃ��̓�����ނ̂��́j�ȊO�ɂ���̂��낤���H
�ƂȂ�܂��B
�@����ł́A3�������ʂƂ͂ǂ̂悤�ȑ��l�̂Ȃ̂ł��傤���B������������I�Ɏv�������ׂ鋅�ʁi�{�[���̕\�ʁA�n���̕\�ʂȂǁj�́A���Ă����悤��2�����̋��ʂł��B3�������ʂƂ́A2�������ʂ̓��������������1�������́A�Ƃ������Ƃ��ł��܂��B
�@�����Ȃ�3�������ʂ̌`���v�������ׂ�͓̂�����߁A������1���Ƃ���2�������ʂ���l���܂��傤�B2�������ʂ�3������Ԃɕ`���ꍇ�A���_���瓙�����i���Ƃ���1�j�ɂ���i���Ȃ킿 x2+y2+z2=1�ƂȂ�j�_�̏W����2�������ʂɂȂ�܂��B
�@3�������ʂ�`���ꍇ�́A2�������ʂ̏ꍇ���玟����1�グ�A4������ԓ��Ō��_���瓙�����ɂ���_�̏W���Ƃ��ĕ`���܂��Bx�Ay�Az��3�����ɉ����Aw��4�ڂ̍��W���Ƃ���ƁAx2+y2+z2+w2=1�ƂȂ�_�̏W����3�������ʂȂ̂ł��B
�@�uw���H����Ȃ��̂��̐��E�ɂȂ�����z���ł��Ȃ��v�Ƃ��������邩������܂���B�m���Ɏ��������Z��ł��邱�̋�Ԃ�3������������܂��A4������z��������@�͂���܂��B�������ɂ�����݂��[���u���ԁv��4�ڂ̍��W�Ƃ��čl����Ƒz�����₷���Ȃ�܂��B
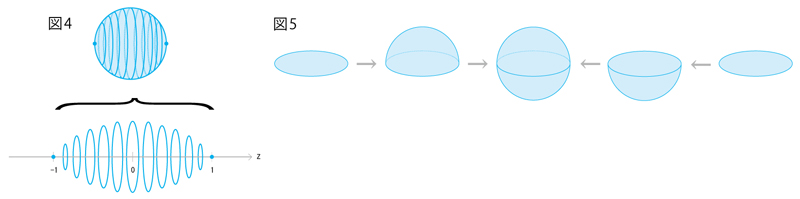
�@���ԂȂ̂�w�̑����t�ƋL���܂��傤�B����t��-1����1�܂œ����ԁA3�������[�N���b�h��Ԃ��v�������ׁA���̂Ȃ��ɂ��錴�_���S�Ŕ��a�� ![]() ��2�������ʂ�z�����܂��B���̎���x2+y2+z2=1-t2�ł�����A��قǂƓ���x2+y2+z2+t2=1�ƂȂ�܂��Bt=0�̂Ƃ����a1��2�������ʂɂȂ�At=�}1�̂Ƃ��ɂ́A���a0��2�������ʁi�܂�_�j�ɂȂ�܂��B�A���I�Ɍ���ƁA���Ԃ�-1����0�܂ł͂���Ƌ��ʂ��傫���Ȃ�A����0�ōő�ɂȂ�A���Ԃ�0����1�܂ł͂���Ə������Ȃ�܂��i�}3�j�B����t=-1����t=1�܂ł�2�������ʂ����ׂđ������킹�����̂�3�������ʂł��B
��2�������ʂ�z�����܂��B���̎���x2+y2+z2=1-t2�ł�����A��قǂƓ���x2+y2+z2+t2=1�ƂȂ�܂��Bt=0�̂Ƃ����a1��2�������ʂɂȂ�At=�}1�̂Ƃ��ɂ́A���a0��2�������ʁi�܂�_�j�ɂȂ�܂��B�A���I�Ɍ���ƁA���Ԃ�-1����0�܂ł͂���Ƌ��ʂ��傫���Ȃ�A����0�ōő�ɂȂ�A���Ԃ�0����1�܂ł͂���Ə������Ȃ�܂��i�}3�j�B����t=-1����t=1�܂ł�2�������ʂ����ׂđ������킹�����̂�3�������ʂł��B

�@�����ׂđ������킹�釁�Ƃ����̂��z�����ɂ�����������܂���B�z�����ɂ����Ƃ��ɂ͎�����1���Ƃ��čl���܂��B1�����̉~���𑫂����킹��2�������ʂ����̂͑z�����₷���Ǝv���܂��i�}4�j�B
�@����1��3�������ʂ̍����́A���g���܂������i���ʂł͂Ȃ��j��2�p�ӂ��A�����̋��ʓ��m��\�荇�킹��Ƃ������@�ł��B�u���ʂ�\�荇�킹��v�̂�3������Ԃł͕s�\�Ȃ̂őz�����ɂ�����������܂���B�����ł������������čl���܂��B���g���܂����~�Ղ�2�p�ӂ��A�����̉~�����m��\�荇�킹�܂��B�~����\�荇�킹�邽�߂ɂ́A�~�Ղ̒��g��3���������ɋȂ��Ă��o�̂悤�Ȍ`�ɂ���K�v������܂��B�������āA2�̂��o�̉��i�~�������j���m��\�荇�킹���2�������ʂ��ł�������܂��i�}5�j�B���l�ɂ��āA2�̋��̋��ʓ��m��\�荇�킹�邽�߂ɂ́A���̒��g��4���������ɋȂ���K�v������܂��B���g��4���������ɋȂ���ꂽ���́A����3������Ԃ��猩��Ƌ��ʂ������c���Ă���悤�Ɍ����܂��i���o������2������Ԃ��猩��Ɖ~���������c���Ă���悤�Ɍ����܂��j�B���̋��ʓ��m��\�荇�킹��̂ł��B
�F���͂ǂ�Ȍ`�����Ă���̂��H
�@�@�|�A���J���\�z��7����~���j�A�����ܖ��̂Ȃ��ŏ��߂ĉ����ꂽ���ł��B�������̂̓��V�A�̐��w�҃O���S���[�E�y�����}���iGrigory Yakovlevich Perelman,1966-�j�ł��B�ނ͂��̌��т�2006�N�Ƀt�B�[���Y�܂����^����Ă��܂����A��܂͎��ނ��܂����B�~���j�A�����܂̏܋�100���h���ɂ������������Ă��Ȃ������ł��B
�@�������A�|�A���J���\�z�̏ؖ����l�ނɂƂ��đ傫�Ȓm�I�i���ł��邱�Ƃ͊ԈႢ����܂���B�������̉F�����r�b�O�o���ɂ���Đ��܂ꂽ���̂ł���A�F���̑傫���͗L���ł���\���������A���Ƃ����āu�F���̉ʂāv�͖��������Ȃ̂ŁA3�������l�̂�p���ĉF���̌`������ł��邩������܂���B���傤�ǁA�L��������ǁu�n�̉ʂāv�������n����2�������ʂł������̂Ɠ����悤�ɁB�|�A���J���\�z���ؖ����ꂽ���ƂŁA�F���̌`�ɂ��Ă̗��_�ɂ���Ȃ锭�W�����҂���܂��B
�g�[���X�N�G�X�g
�@�݂Ȃ����RPG�i���[���v���C���O�Q�[���j�ȂǁA��ʂ̒��̐��E��`������Q�[���ŗV���Ƃ�����ł��傤��
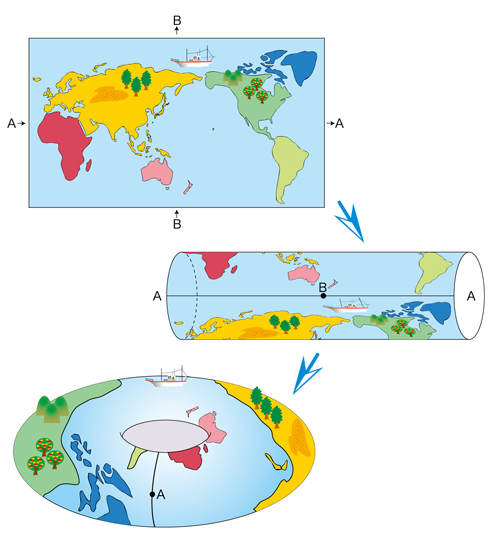
�@�����̑�����1�̕����ɂ����Ɛi�ނƁA��ʂ��X�N���[�����āA�₪�Č��̈ʒu�ɖ߂��ė��܂��B���ɂ����Ɛi�ނƃ}�b�v�̓��̒[���琼�̒[�֏o�Ă��܂��B����́A���������Z�ޒn���Ɠ����Ȃ̂ł����A�k�ɂ����Ɛi�ނƃ}�b�v�̖k�̒[�����̒[�֏o��ꍇ�����������܂��B���������ɐi��ŏo���_�ɖ߂��Ă��铹�ƁA��k�����ɐi��ŏo���_�ɖ߂��Ă��铹�Ƃ��A�o���_�ȊO�Ō����Ȃ��̂ł��B�����l����ƁA����͎������̒n���Ƃ͈���Ă��܂��B�n���ł́A��k�����ɐi��ň��肷�铹�ƁA���������Ɉ��肷�铹�Ƃ́A�K��2�����邩��ł��B
�@����ł́A�����ɂ���k�ɂ��}�b�v�������Ƃ��A���̃}�b�v�͂ǂ�Ȍ`�������V�̂�\�킵�Ă���̂ł��傤���B�܂��A�}�b�v�̖k�̒[�Ɠ�̒[�������ƌ��Ȃ���̂ŁA������\�荇�킹�܂��B����ƁA���̂悤�Ȍ`�ɂȂ�܂��B����ɓ��̓��̒[�Ɛ��̒[�������Ȃ̂œ\�荇�킹��Ɓc�c�g�[���X���o���オ��܂����B������RPG�̎�l�������̓g�[���X�̏��`�����Ă���̂ł��B

���w���@�����Ȋw�ȁ@�R�c�@�C�i ����
- �v���t�B�[��
-
���w���m�B���͌��іڗ��_�A3�������l�̘_�B���іڗ��_�Ƃ́A�ւɂȂ��Ă���R��������̂��ǂ����𐔊w�I�ɏؖ����悤�Ƃ���w�╪��B�����A���w�҂̒m�I�D��S�����Ŏn�܂������삾���A���݂ł�DNA�̍\����F���_�Ȃǂւ̉��p�����҂���钍�ڂ̕���B�R�c�搶�̓R���s���[�^���g�������іڗ��_�̌����ɂ��ڂ����B�ʑ��w�̕���ɏd�v�ȕ��������˂�Ɓu���ϕ��͈Ӗ����炢��m���Ă����������ǁA�x�N�g���Ɨ��̐}�`�͂������藝�����Ă����Ă��������v�Ƃ̂��ƁB���Q�������R�����ZOB�B
