理学部 数理科学科 山上　敦士准教授

革命を志した青年が起こした数学上の一大革命

　19世紀前半のフランスは革命の反動で王制へと復古し、政治のあり方を巡って民衆と政府が対立する不穏な時代でした。この時代のフランスに現れた数学者エヴァリスト・ガロア（Évariste Galois、1811-1832）も王制に不満を持ち、王制に批判的な態度を示しては何回か牢獄にも入れられました。ガロアは二月革命によって樹立する第二共和制（1848年成立）を見ることなく、わずか20歳で若い命を失いました。しかしながら、彼は数学の世界では大革命ともいえる業績を残したのです。ガロアが残した成果の一端について山上先生にご紹介いただきました。

古来mathematicsはmagicだった！？

　2次よりも大きい高次の方程式は単純な係数を持つものであっても、簡単に解ける※1ようには見えないと思います。3次方程式と4次方程式については解の公式が知られているため、公式を使って解くことができます。3次や4次方程式について解の公式が発見されたのが16世紀。それ以前は高次の方程式といえばパズルのように難解なものでした。友人やライバル同士で方程式を出題し合い、どちらが先に解くことができるのかを知的なゲームとして楽しむことも行われていました。

　高次の方程式を解くことは、当時の一般の人にとってはまるで魔術のように感じられていて、数学は魔法のような不思議なものだと思われていました。現代のみなさんが、数学の教科書を携えて16世紀以前のヨーロッパに行くことができれば、立派な魔術師になれるかもしれません。

　16世紀以降の代数を研究する数学者にとって、5次以上の方程式を解く公式の発見は大きな関心事となっていました。4次までの方程式には解の公式があるわけですから、5次以上の方程式にも解の公式があるに違いない、と多くの数学者は考えていました。

　この問題に結論が出たのは、19世紀に入ってからのことです。フランスの数学者エヴァリスト・ガロアが提案した理論によって、新たな展開がもたらされました。ガロアは5次以上の方程式に解の公式がないことをより洗練されたかたちで証明し、どんな場合に方程式が解を持つのかを示しました。※2

※1　ここで「解く」ということは、その方程式の係数たちの四則演算とべき根（平方根√や3乗根 ³√など）によって表された解を見つける、ということ

※2　5次以上の方程式が一般に解の公式を持たないことを最初に証明したのは、ガロアと同時代のノルウェーの数学者、ニールス・アーベル（Niels Abel、1802-1829）

不遇の天才ガロア

　　ガロアは若くして亡くなった数学者でした。恵まれた数学的才能とは裏腹に、教師たちはガロアを高く評価しませんでした。17歳のときに書いた素数次方程式の解き方についての論文はフランス学士院に提出はしたものの審査官に紛失されてしまい、希望していたエコール・ポリテクニークへの入学試験にも2度失敗します。1831年に記した論文（後の「ガロア理論」）は、当時の一流の数学者たちにとっても難しい内容だったため、数学の歴史を変えるほどの価値があるにも関わらず、書き直しを求められています。このように、ガロアは正当な評価を得ることがないまま、翌32年に決闘によって命を失ってしまったのです。※3

　　もちろん、現在ではガロアの業績は正しく評価されています。短い人生の間に綴ったいくつかの論文の中に、現代数学にとってたいへん重要な成果が詰まっていました。中でも最大の業績は「群論」の導入です。群論はその後の科学の発展になくてはならない理論で、相対性理論や量子力学にも必要不可欠なものでした。

※3　決闘の原因については「ある男性と一人の女性の奪い合いになったため」とも「政治活動を巡る陰謀」とも言われている。

群の性質から方程式の性質が分かる

　ガロアが注目したのは、方程式の解を互いに置き換える操作（置換）を群※4として考え、この置換群（後のガロア群）の性質を調べることで方程式が係数の四則演算とべき根だけで解けるかどうかを判定できるのではないか、ということでした。

　たとえば、3次方程式の3つの解X₁、X₂、X₃を考える場合、この3つの解を置換する方法は最大で6通りあります（下図）。このように、n次方程式の可能な置換はn!通りあることになります。調べる方程式の種類によって、また解にどこまでの数を含めるのか（たとえば有理数に加えても許すなど）によって、n !通りのうちのどれを元とした置換群になるのかが変わってきます。

　ある方程式が解けるのであれば、その方程式の置換群は一定の条件を満たすのですが、一般に5次以上の方程式は、その置換群が条件を満たさないことが分かっています。※5

　群の導入により、数学は解そのものではなく、「解の置き換え」のような操作をも扱えるようになりました。この新しい考え方によって数学の世界はより自由になり、大きく広がったのです。

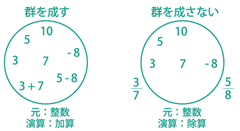
※4　群とは、数や記号の操作などを元（構成要素）として持ち、元に何らかの演算をほどこすことのできるグループのこと。たとえば「元は整数、演算は加算」は群を成すが、「元は整数、演算は除算」は演算結果が整数とは限らないため群を成さない。置換群の場合「元は置換、演算はある置換に続けてさらに置換を行うこと」になる。

※5　群の中にはその一部分がそれ自体で群となるものがある（部分群）。そのうち極大不変真部分群とは、もとの群を除いた群（真部分群）の中でそれより大きなものがなく（極大）、もとの群の元によって変換しても部分群全体が変わらない（不変）もの。（不変部分群は正規部分群とよばれることもある。）群Gの極大不変真部分群Hをとり、またHの極大不変真部分群Kをとり、というように、極大不変真部分群の元の個数が1になるまで、極大不変真部分群をとる作業を繰り返したときに、それらの元の個数をそれぞれ小文字で、g、h、k、…として、g÷h、h÷k、…がすべて素数である場合、群Gは可解群と呼ばれる。ある方程式の置換群が可解群となる場合、その方程式は係数の四則演算とべき根により解くことができる。

正n角形を定規とコンパスだけで描けるか？

　方程式が解けるのか解けないのかが判別できることで、わたしたちは、ある図形をコンパスと定規を使って描くことができるのかどうかを知ることができます。

　長さ1が決められれば、コンパスと定規とを使うことであらゆる有理数の平方根√　と四則演算を繰り返し用いて得られる長さ（たとえば）を描くことができます。言い換えれば、コンパスと定規で図形を描くということは、有理数の平方根√　と四則演算を繰り返し用いて得られる長さによって図形が表されているということと同じなのです。

　このことから、図形を表す方程式が有理数の平方根√　と四則演算を繰り返し用いて得られる解を持たないと分かれば、その図形はコンパスと定規では描けないということが分かるのです。

　正三角形、正四角形、正五角形、正六角形などは、ガロアの理論を持ち出すまでもなくコンパスと定規で作図可能だと知っていると思います。では正七角形は？　正十角形は？

　実はガロアの理論から導かれる結論を言うと、コンパスと定規で作図可能な正多角形は以下の3通りだと分かっています。

α　正2ⁿ角形
β　正2^m+1角形（ただし素数のみ）
γ　正2ⁿ(2^m+1) 角形（ただし、2^m+1 は素数）

　βがm=1のとき3、αがn=2のとき4、βがm=2のとき5、γがn=1かつm=1のとき6…と続いて行きます。この3つの式から7は出てこないため正七角形は作図不可能ですが、正十角形はγがn=1 かつm=2のときに10となり作図可能と分かるのです。

　この計算を続けていくと、なんと正十七角形は作図可能ということになります。正十七角形の作図方法はドイツの数学者・物理学者カール・フリードリヒ・ガウス（Carl Friedrich Gauss、1777-1855）が1796年に発見しました。正素数角形の作図は正三角形と正五角形しかできないと考えられていましたから、何世紀かぶりの快挙でした。朝目が覚めたときに作図方法を閃いたそうです。ガウスが19歳のときのことです。

時代を超越する数学

　話をガロアに戻しましょう。ガロアの理論は彼の死後、数学や物理学の世界でその重要性を高めていき、ついには近年の数学史上の一大事件である「フェルマーの最終定理の証明」を解くためのカギとなりました。

　フェルマーの最終定理とは、Xⁿ+Yⁿ=Zⁿという式において、X、Y、Zが0以外の整数のとき、n≧3（nは自然数）では解が存在しない、という定理です。この定理の証明は「X、Y、Zに解が存在すれば矛盾する」ことを示す方法で行われました。解X=a、Y=b、Z=cを仮定し、a、b、cを用いて作られる楕円曲線に付随するガロア表現を深く考察することで、矛盾が導かれることが証明されたのです。

　この問題をフェルマーが書き記したのが1637年頃。ガロアの没年は1832年。そしてイギリスの数学者アンドリュー・ワイルズ（AndrewWiles、1953-）により証明がなされたのは1995年。300年以上もの年月を超えて、数学の天才たちが協力し合った結果、人類は新たな証明を手に入れました。偉大な数学の成果は容易に時代を超えるのです。

アドバイス

必ずしも解けなくてもいい取り組むこと、質問することを大切に

　数学を苦手だと言う人には、苦手だという気持ちばかりで練習問題に取り組もうとしない、周りの人に質問しないという場合が多いように思います。できても、できなくてもまずは挑戦することが大切だと思います。

　特に数学の道を志すならば、先生が「何番と何番の問題をやっておきなさい」と言ったとしても、問題集に載っているすべての問題に貪欲に取り組もうという姿勢を身につけてください。問題文の文中にも別の問題がかくれていることがあります。そういったものを無視せずに積極的に取り組んでください。そして、数学の得意な友人や先生に質問をぶつけて、常に聞く癖を持ってください。必ずしも解けなくてもいいのです。この繰り返しが必ず成長の糧となるのです。