理学部　数理科学科　森　隆一教授

　コンピュータの発達は数学の世界にも大きな影響をもたらしました。コンピュータがなかった時代には、複雑な現象やランダムな現象は、数学のモデルとして考えることはできても、答えを具体的に求めることは難しいものでした。簡単な微分方程式でも解の値を求めるには膨大な計算が必要となります。もともと、コンピュータはこのために開発されたものといえ、数値解析は現代の産業において不可欠なものとなっています。コンピュータの性能が向上するとともに、以前は難しいものだったさまざまな現象が、数学の問題として扱えるようになったのです。そして、数学とコンピュータとの新たな展開において重要な役割を担ったのが、確率論の分野でした。確率論がご専門の森隆一先生に、コンピュータを使って解く数学の世界を、さまざまな応用例を交えながらお話いただきました。

現実世界と数学とを結ぶ

　　私たちの身の回りには、「答え(解)があることは明らかなのだけれども、それを具体的に求めることは非常に難しいもの」や｢仕組みが複雑で分からないもの」が数多くあります。後者の多くはランダムな現象として扱われています。

　　答えはあるが求めることが難しいものとしては、「将棋や囲碁の次の一手」のように膨大な可能性の中から最適な1つを選び出すような問題があり、ランダムな現象としては、天気、人口動態や売り上げ予測、株価の動向などがあります。

　このような問題や現象を扱うとき、確率論が役立つ例をいくつか挙げることができます。

モンテカルロ法

　　数学的な仕組みが難しいものやランダムな現象を、実際に確率モデルとして計算するとき、コンピュータで乱数を発生させ、それを用いてシミュレーションを繰り返します。このような方法を「モンテカルロ法」と呼びます。モンテカルロ法は「コンピュータの父」と言われる数学者ジョン・フォン・ノイマン（John vonNeumann　1903-1957）が考案した方法です。中性子が物質の中を動き回る様子を研究するために考え出した方法に「モンテカルロ」という暗号名を付けたことが起源になっています。

　実際に、シミュレーションを使ってどのように数学の問題が解かれるのか、その具体的な手順を「巡回セールスマン問題」と呼ばれる問題を例として見てみましょう。

巡回セールスマン問題の解き方

　　「巡回セールスマン問題」は「解の存在は明らかであるけれども、その値を求めるには膨大な計算が必要となるもの」の典型で、N個の町を重複なく訪れ出発点に戻ってくるセールスマンの最適な（移動距離とか費用などのコストが最小となる）経路を求める問題です。私たちは日常、この種の問題を直感的に解いています。たとえば、京都を出発地点として、札幌・仙台・東京・名古屋・大阪・福岡の6都市を巡回する場合、札幌の次に福岡に行き、それから仙台に行くというルートは、距離や費用がかかると直感で分かるのではないでしょうか。ところが、この問題を解く確実な方法は、すべての可能なルートに対してそのコストを計算し、最小値を求める方法です。したがって、訪れる都市の数が増えれば増えるほど、計算に時間がかかります。（経路の総数が N! 個となることは組み合わせで習います。）

　このような問題では、モンテカルロ法の１つである、シミュレーティッド・アニーリングと呼ばれる方法により、最適な解に近づくことができます。初めは適当な経路を選びます。その後、以下の操作を繰り返します。まず、訪れる順序を少し変えた経路をランダムに選び、新しい経路のコストを計算します。そして、新しい経路のコストが、前のものより、低い場合は新しい経路に変更し、新しい経路のコストが高い場合には、コストの差により、確率的に変更します※1。

　この、「ランダムに選ぶ」→「比較する」→「低コストであれば変更、コスト高であれば確率的に変更」を何度も繰り返すと、求める最適解に近づくのです。

※1 「比較してコストが高い場合にも、コストの差により確率的に変更する」という手順に疑問があるかもしれない。この手順がなぜ必要かということを分かりやすく言うと次のようになる。
　コストの高い経路から、よりコストの低い経路に変更しながら答えを探す、という作業は、高い山の上からより低いところへと降りていく行為に似ている。山が1つしかない場合には、ただ単純に降りていけば一番低いところまでたどり着けるが、現実の問題では、山も谷もたくさんあるような状態が一般的だ。このような場合、1つの谷に降りてきて、周囲にそれ以上低いところがないからといって動くのを止めてしまうと、他にもっと低い谷があっても、決してその谷にたどり着けない。一番低い谷に降りるためには、ときには山に登りなおすことも必要となる。そのため、コストの高い経路へもいくことを可能にすることが、この方法のポイントであり、「確率的山登り」という名前がついている。

さまざまな現象への応用

　モンテカルロ法を用いた応用例は、実に多種多様で、巡回セールスマン問題以外にもさまざまな現象に応用されています。以下にそのユニークな例を紹介しましょう。

1.デパートではぐれたときの再会確率

（この問題は、あるスーパー・サイエンス高等学校において、生徒が自ら課題としてとりあげたものです。）

　デパートや百貨店で買い物をしているときに、友だちや家族とはぐれてしまったという経験はありませんか？ そういう場合、一方が一箇所にじっとして、もう一方が探して動き回るのがいいのか、それとも、お互い探して動き回るほうがいいのか、みなさんはどちらが早く再会できると思いますか？

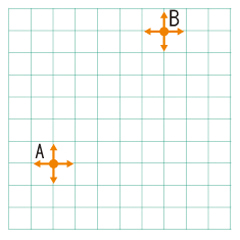
　この問題は、確率のモデルとして考えることができ、シミュレーションは次のようになります。デパートの1フロアを碁盤の目のように区切られた矩くけい形と考え、その矩形上に2つの点A・Bを配置します（下図）。点の動きは乱数によって、上下左右それぞれ の確率で決めます。2つの点が同じ座標になるとプログラム終了で、終了するまでの移動回数を測定します。最初は、一方が一箇所にじっとしている場合、つまり、点Aだけを動かすシミュレーションを行い、次に点A・Bの両方を動かすシミュレーションを行います※2。

　実は、このシミュレーションの結果は、点Aだけを動かした場合と、点A・Bの両方を動かした場合とでほとんど差が出ません。つまり、探す方向をランダムに決めるのであれば、一方がじっとしていても、お互い探し回っても再会する確率は同じになるのです。矩形の辺に到達した場合の処理は問題となります。

※2　ロール・プレーイング・ゲームはこのモデルを目茶苦茶複雑にしたものといえるが、確率を計算することは殆ど不可能である。しかし、シミュレーションは可能で、実際、多くの人がシミュレーションを実行している（ゲームで遊んでいる）。この場合は、1回のサンプルを得るのに時間がかかり過ぎる。

2.複雑な図形の面積を求める

　図形の面積もコンピュータによるシミュレーションで求めることができます。もちろん、三角形や長方形といったシンプルな図形であれば、辺の長さや角の大きさから簡単な計算で求められるので、わざわざシミュレーションするまでもありませんが、複雑な図形の面積を求める場合には有効な方法です。

　具体的には、面積を求めたい複雑な図形を含む矩形を考えます（下図）。そして、2つの一様な乱数をもとにx、yの2つの数値を作り、その(x,y)から1つの点を決めます。この点(x,y)が図形の内側にあるのか、外側にあるのかを判定します。この手順を何度も繰り返せば、全体の点の数と内側にある点の数の比が、矩形の面積と求めたい複雑な図形の面積の比となり、そこから図形の面積が求まります。でたらめにダーツを投げて図形に当たった回数を数える方法と考えれば分かりやすいでしょう。

3.ギャンブルは必ず負ける

　高校生のみなさんはまだギャンブルをしてはいけませんが、法律上できる年齢になっても、しないほうが賢明だということがシミュレーションの計算結果から分かっています。

　ギャンブルの1回1回の勝敗を乱数によって確率で決めるとします。通算して考えると「負け」とは、自分の財産が0になるときで、「勝ち」とは、自分の財産が0にならないで最初の所持金を越えている場合と考えることができます。

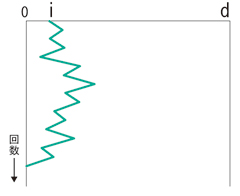
　自分の所持金をi、胴元（ギャンブルの運営側）の所持金をdとし、自分または胴元の所持金が0となるまで続けるとします。多くの場合、圧倒的にdのほうが大きい。1回1回の勝敗が確率によるものなので、iの位置からスタートしてdに行き着くことはまずありません。ほとんどの場合、0に行き着いて終わりとなります（下図）。

　つまり、大きな胴元が運営するギャンブルは、ある一時期はiを越えている（勝っている）時があったとしても、それは一時的なものであり、何回も繰り返すと必ず0に到達する（負ける）ゲームなのです。（このモデルでは、自分の所持金が0となる確率はとなります。）

現実と理論を結ぶ実験数学

　コンピュータの登場により、数学が扱える現象は飛躍的に増えています。従来、ランダムな現象を数学的に取り扱うことは、現実的なモデルでは困難でした。また、星の軌道計算のように、自然や社会における現象を微分方程式系で表し、その解をもとに現象の解析も行われています。この場合も、解を具体的に求めるには膨大な計算が必要となり、コンピュータによる計算が必要不可欠になります。これまで見てきたように、答えを具体的に求められない現象であっても、シミュレーションという形で数学の俎そじょう上に乗せることができるのです。これによって、フラクタル（部分と全体が自己相似となるような図形）のように、新たな理論が展開されることも少なくありません。このような数学の手法は「実験数学」とも呼ばれています。今後、実験数学はさらに広い分野に応用されていくことでしょう。

トピックス

数の知識で秀吉を慌てさせた知恵者

　安土桃山時代の鞘さや職人で噺はなしか家でもあった曽呂利新左衛門は機知とユーモアに富んだ人物として有名で、数の性質を利用して、時の権力者・豊臣秀吉を慌てさせたという逸話が残っています。

　ある時、曽呂利新左衛門の功績に対して、秀吉が「何でも褒美をあげよう、何がよいか？」と聞くと、新左衛門は「今日は米1粒、明日は米2粒というように、前の日の2倍だけの米粒を将棋盤の目の数（81）の日数だけもらいたい」と答えました※3。最初、秀吉はたったそれだけでいいとは無欲な奴だと思ったそうです。

　最初は本当にわずかな褒美でした。2日目2粒、3日目4粒、4日目8粒、10日経っても2⁹=512粒にしかなりません。ところが、さらに日が経つにつれ、褒美の米粒は膨大な量になっていきました。20日目には2¹⁹=524288粒。米1000粒が約23グラムなので、約12キログラムになります。一ヵ月後（30日目）には229 =536870912粒で約12.3トン。一人の人間が一年間に食べる米の量が約60キログラムなので、200年間以上食べ続けられる量です。そして、81日目には、約2.8×10¹⁶トン。世界人口65億人が7000万年間食べ続けられる量となります。豊臣秀吉といえどもこの褒美を与えることはできませんでした。

※3　一ヶ月分とも百畳間（秀吉自慢の大広間）の畳の数である100日分とも言われる。ちなみに100日目は、約146×10²⁰トン。重さで地球2つ分より多量の米が必要となる。