素数の不思議な性質

　素数とはそれ以上分解することができない、整数の世界の元素と言えます。英語ではprime numberと言われ、素数の位置づけがよく言い表されています。このように言われるのは、あらゆる整数が、どんなに大きな数であっても、素数の積によって表すことができるからです。みなさんも既に習った素因数分解とは、まさに整数を素数の積で表すことなのです。このことから、「数とは何か？」という問いに対して考えるためには、その構成因子である素数の性質を知ることが欠かせません。まずは、素数が持つ不思議な性質を4つ紹介しましょう。

素数はいくつあるのか？

　数を構成する素という重要なものでありながら、数の中に現れる法則が定かではない素数ですが、ある程度大きなスケールで見ると、現れ方に規則性のようなものが出てきます。しかしながら、この規則を正確に捉えるのは難しく、1からある任意の数までにいったいどれぐらいの素数があるのか、という問題も整数論の難問とされています。
　1からxまでの素数の個数を表す式をπ(x)と表記します。
π(x)については

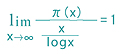
　が成り立つことが分かっています（素数定理）。つまり、xが十分に大きいとき、π(x)は、およそとなるのです。「およそ」と言うのは、xに有限の数を当てはめた場合、必ず誤差が生じるからです。π(x)を厳密に定義する式は現在のところまだ解明されていません。

ゼータ関数とリーマン予想

　ドイツの数学者リーマンは、π(x)とのズレ（誤差）を表す公式を発見しました。この公式が成り立つためには、リーマン予想が正しいことが証明されなければなりません。
　リーマン予想とは、ゼータ関数と呼ばれる関数についての予想で、1859年にリーマンが彼の論文の中で予想して以来、現在にいたるまで証明されていない問題です。世界の数学界においても難問中の難問とされていて、アメリカのクレイ研究所が2000年にミレニアム懸賞問題として、解決者に対して100万ドルの懸賞金を支払うと公約しています。
　ゼータ関数とは、18世紀半ばごろにオイラーが特殊な性質があることを見つけ出した無限級数のことで

と無限に加算する形の式です。
　この関数はsが2,4,6などの場合、特殊な値をとることが分かっていて

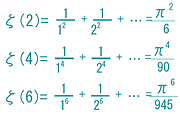
という値になります。
　また、sが負の偶数のとき、ζ(s)= 0となります。この偶数値をリーマン・ゼータ関数の「自明な零点」と呼びます。
　リーマン予想とは、この零点に関するもので、

自明な零点以外でゼータ関数が0になるのは、（yは実数）のときのみである。

　というものです。ゼータ関数は素数の分布状況を表しており、19世紀末にζ(1+iy)≠0が証明されています。このことから素数定理が導かれます。

交通安全のお守りにもなる？リーマン予想

　100万ドルの懸賞金がかけられているリーマン予想ですが、この問題の難しさを表すエピソードとして、次のようなものがあります。19世紀後半から20世紀前半のイギリスの数学者ハーディーは、当時まだ事故が多く危険な乗り物だった船に乗る前には必ず、「私はリーマン予想を解いた」という嘘の手紙を書いて友人に送ったそうです。ハーディーがもしも海難事故で死ぬと「リーマン予想を解いた数学者」としてたちまち数学史上の英雄になってしまうから神様がそれを許さない（＝死なせない）はずであり、そうならないならば神様はいないということになり、無神論者だったハーディーにとっては自らの信念の証明になります。この手紙は「ハーディーのおまじない」と呼ばれていますが、リーマン予想を解くことが彼のような著名な数学者にとってすら困難だということが垣間見える話ですね。

女王は働かない？

　「数学の女王」と言われる整数論は、数学の最古の分野でもあります。私たち人類は古くから数の概念を持っていました。そのため、古代ギリシャの数学者も素数に関して様々な考察を行っています。しかし、素数について、私たちの知見が飛躍的に向上したのは、比較的新しい数学の他の分野（微積分、関数論や代数学）での発展があったからなのです。これらの分野の成果が整数論の発展にも大きく寄与しています。逆に、整数論の成果は数学の他の分野にあまり貢献していないと思われています。整数論が「数学の女王」と呼ばれる理由には、理論の美しさや純粋さだけではなく、「他の分野の貢献は受けるけれども自分は他の分野に貢献しない」という皮肉も込められているのかもしれません。

みんなのパソコンで大きな素数を見つけよう? −　GIMPS

　とにかく数学が大切です。これが解らないと物理は解りません。ただ、“光”で必要な数学の領域は限られていますし、計算もそんなにややこしいものは必要ありません。

　2n-1の形で表せるメルセンヌ素数は、何万桁にもなる大きな素数を発見する手段として有効で、現在もコンピュータを使ったメルセンヌ素数発見のプロジェクトが進められています。

　このプロジェクトの名称はGIMPS（Great Internet Mersenne Prime Search） といいます。世界中のコンピュータに少しずつ分けて計算をしてもらい、トータルで膨大な計算をやってしまおうというプロジェクトです。GIMPSには、インターネットに接続されているパソコンがあれば誰でも参加できます。

　これまでにGIMPSによって発見されたメルセンヌ素数は2006年9月現在で10あり、最大のものは2^32,582,657-1です。この素数は約980万桁です。大きな素数を発見する技術は、暗号技術と深い関係があり、技術発展の促進のため1000万桁を超える素数の発見には10万ドルの賞金がかけられています。

理学部･数理科学科 村瀬 篤教授

プロフィール

　専攻は多変数保型形式の整数論。講義では暗号についても教えていて、卒業研究では暗号解読プログラムなども指導する。北海道育ち、札幌南高校OB。中学時代の数学の先生から高校の数学を先取りして教わり、数学の面白さに興味を持つようになる。その経験から、高校時代に大学の数学を独学で学んだという。